|
A
idéia básica ao lidarmos com as lentes, e que nos permite determinar
a localização da imagem, é que a imagem formada pelo primeiro dioptro
se torna o objeto para o segundo dioptro.
Vamos
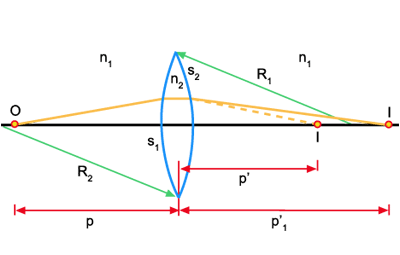
considerar um objeto O diante de uma lente de acordo com a figura
abaixo. A imagem
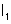conjugada pelo primeiro dioptro (de raio
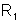) tem abcissa
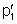de tal forma que utilizando a equação anteriormente obtida
para um doptro esf[erico
.
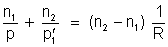A
imagem
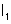é o objeto (virtual nesse caso) para o dioptro de superfície
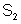com raio
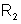. Para essa superfície temos (lembrando que o objeto é agora
virtual para a superfície
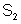e que
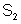é negativo)
.
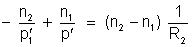Somando
agora as duas últimas equações obtemos
.
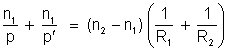Dividindo
a equação anterior por
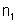obtém-se
.
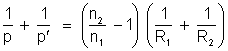Esta
equação é conhecida como equação dos fabricantes de lentes. Ela se
torna inteiramente análoga à equação dos espelhos esféricos se definirmos
a distância focal f através da relação
.
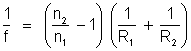A
equação acima é conhecida também por equação dos fabricantes de lentes.
Utilizando essa equação teremos, com essa definição, a equação
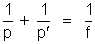
que
é uma equação análoga aos espelhos esféricos.
No
caso em que uma das superfícies for plana, a equação se aplica igualmente,
ela é até mais simples nesse caso, pois, basta tomarmos o raio de
uma delas tendendo ao infinito. Por exemplo, se o primeiro dioptro
for plano e o segundo for esférico de raio R a equação dos fabricantes
se torna
.
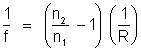A
relevância da distância focal de uma lente pode ser analisada quando
consideramos raios incidentes paralelamente ao eixo principal de uma
lente. Nesse caso as lentes se dividem em duas categorias. Nas lentes
convergentes os raios convergem para um ponto (o foco da lente).
Este é o significado físico da distância focal. Ela nos dá a que
distância da lente haverá a convergência dos raios paralelos. As
lentes de borda fina são convergentes.
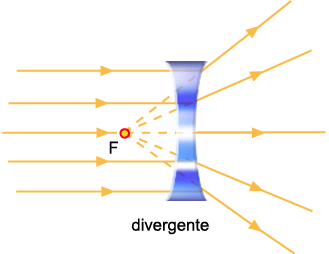
Se
a lente for divergente então os raios refratados não convergem para
um ponto. No entanto, o prolongamento desses raios converge num ponto
– o foco. As lentes de borda espessa são divergentes.
Tomemos,
para ilustrar esse ponto, o ponto p tendendo para infinito (os raios
vão agora se tornando paralelos). Para um objeto no infinito
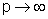a imagem acontece no ponto
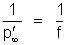
ou
seja, a imagem está no foco.
Lentes convergentes têm a distância focal positiva e lentes divergentes
têm a distância focal negativa.
|
