|

Para
procedermos ao estudo analítico do processo de formação de imagem
numa lente, vamos estudar a imagem de um objeto puntiforme diante
de um dioptro esférico. Os dois meios transparentes serão assumidos
possuindo índices de refração
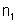 e
e
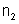 e separados por uma superfície esférica de raio R. O objeto
está no ponto O e a imagem se formará no ponto I o qual se encontra
no eixo passando pelo centro de curvatura C e o objeto O. As coordenadas
da imagem I e do objeto são p e
e separados por uma superfície esférica de raio R. O objeto
está no ponto O e a imagem se formará no ponto I o qual se encontra
no eixo passando pelo centro de curvatura C e o objeto O. As coordenadas
da imagem I e do objeto são p e
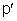 .
.
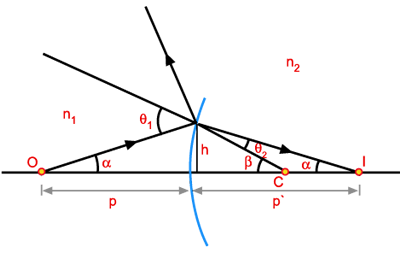
Consideremos
primeiramente um raio incidente proveniente de O formando um ângulo
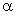 com a horizontal e
com a horizontal e
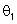 com a normal à superfície. Este raio é refratado formando
um ângulo
com a normal à superfície. Este raio é refratado formando
um ângulo
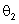 com a normal e um ângulo
com a normal e um ângulo
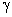 com a horizontal. O
conjunto de raios refratados formará a imagem em I do objeto.
com a horizontal. O
conjunto de raios refratados formará a imagem em I do objeto.
Admitiremos
que todos os ângulos são pequenos e que, portanto, as seguintes aproximações
são válidas:
De
acordo com a Lei de Snell teremos
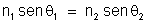 .
.
Admitindo
que os ângulos são pequenos, teremos uma relação simples entre os
ângulos
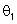 e
e
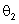 :
:
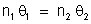 .
.
Lembramos
agora que num triângulo qualquer um ângulo exterior é igual à soma
dos ângulos interiores opostas à ele. Se aplicarmos esse resultado
para os triângulos OPC e IPC podemos afirmar que valem as relações
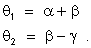
Usando
a Lei de Snell para ângulos pequenos e substituindo
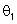 e
e
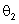 por esses valores temos
por esses valores temos
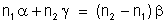 .
.
Utilizando
a seguir as aproximações mostradas acima para
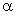 , ,
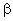 e
e
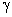 teremos
teremos
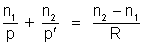 .
.
Vemos,
assim, que essa equação tem uma certa semelhança com a equação para
os espelhos. A convenção dos sinais das coordenadas é a seguinte:
p é positivo se o objeto estiver na frente da superfície
(objeto real)
p é negativo se o objeto estiver atrás da superfície (objeto virtual)
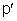 é positivo se a imagem estiver atrás da superfície (imagem
virtual)
é positivo se a imagem estiver atrás da superfície (imagem
virtual)
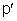 é negativo se a imagem estiver na frente da superfície (imagem
real)
é negativo se a imagem estiver na frente da superfície (imagem
real)
R é positivo se o centro de curvatura estiver atrás da
superfície
R é negativo se o centro de curvatura estiver na frente
da superfície.
|