| |

| A
máquina de Atwood é um dispositivo bastante simples
e que permite, pela determinação da aceleração
dos corpos em movimento, testar as leis da mecânica. Ela
consiste de dois corpos de massas m1
e m2 presos por
um fio que passa por uma roldana. Nos problemas mais simples
simplificamos o problema admitindo que ela não tenha
massa. Isso é claramente uma aproximação.
A roldana tem um momento de inércia dado por
e devemos então levar em conta o seu movimento de rotação.
Assim, além das equações usuais do movimento
das partículas de massa m1
e m2
onde
T1 e T2
são as forças tensoras nos fios , temos agora
a equação de movimento da roldana |
|
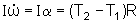
.
Note-se
que T2 = T1
só é possível se desprezarmos a massa da roldana.
Lembrando que
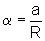
,
temos
de
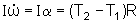 e
e
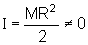 que
que
 .
.
A solução
torna-se agora, utilizando as equações
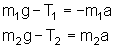
 ,
,
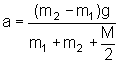 .
.
Se tomarmos inicialmente as duas partículas em repouso e a
mesma altura (z = 0) teremos para a energia total
E
= 0
Quando elas se deslocam de uma altura h em relação à
posição original, a energia será

E portanto,
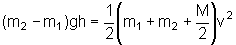
Donde obtemos
que
 .
.

|
|