|

A
análise das colisões elásticas no caso geral
fica enormemente facilitada pelo uso do sistema centro de massa e
o uso das coordenadas em relação a esse sistema (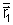 e
e
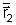 ).
Lembrando que em relação ao centro de massa. ).
Lembrando que em relação ao centro de massa.


|
e que a
coordenada relativa é definida por
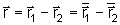 ,
,
temos
|
|
e, portanto, as
velocidades das duas partículas relativas ao centro de massa
são:
| |
e |
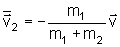 ,
, |
onde
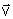 é a velocidade de m1 com respeito a m2.
é a velocidade de m1 com respeito a m2.
Numa
colisão elástica, a conservação
da energia cinética nos leva a

onde
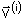 e
e
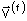 são as velocidades relativas no estado inicial e no estado
final e
são as velocidades relativas no estado inicial e no estado
final e
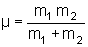
é a massa
reduzida. Temos, portanto
e
consequentemente, só existe uma mudança de direção
na velocidade relativa. Escrevemos, portanto
onde
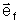 é um versor que indica a direção na velocidade
relativa no estado final.
é um versor que indica a direção na velocidade
relativa no estado final.
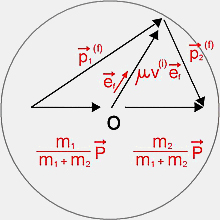
A partir desses resultados podemos escrever
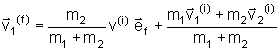 ,
,
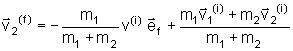 , ,
onde o último
termo é a velocidade constante do centro de massa.

Portanto,
onde
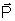 é o momento linear total (constante) em relação
ao sistema de laboratório.
é o momento linear total (constante) em relação
ao sistema de laboratório.


Utilizando vetores,
temos o seguinte diagrama para as equações acima:
Se
uma das partículas (digamos a partícula 2) estiver em
repouso, temos as três possibilidades abaixo:
Os
ângulos
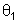 ,
e ,
e
 são
ângulos de espalhamento da partícula 1 como vistos nos
dois sistemas. O ângulo são
ângulos de espalhamento da partícula 1 como vistos nos
dois sistemas. O ângulo
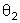 é o ângulo de recuo da partícula 2 no sistema
de laboratório.
é o ângulo de recuo da partícula 2 no sistema
de laboratório.
Os diagramas das figuras anteriores são muito úteis
para obtermos todos os parâmetros a partir de apenas um, dado
como conhecido.
Por exemplo, uma simples inspeção geométrica
nos fornece a seguinte relação entre os ângulos
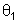 , e , e
 . .
Vemos também
que
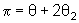
istó
é,
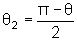 .
.
Tomando
o quadrado de
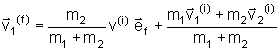 e
e
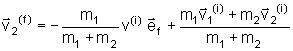
vemos que
e
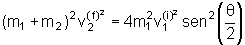 .
.
Vamos
analisar os três casos relevantes.
a) m1
> m2
Observando
a figura notamos que, nesse caso,
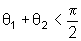
e
o ângulo 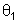 atinge um valor máximo dado por
atinge um valor máximo dado por
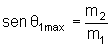 |
|
b)
m1 < m2
Nesse
caso a velocidade
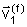 da primeira partícula pode ter qualquer direção.
Nesse caso
da primeira partícula pode ter qualquer direção.
Nesse caso
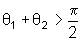 |
|
c) m1
= m2
Todas
as equações e resultados se simplificam. Olhando
para a figura vemos que
De
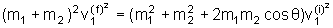
e
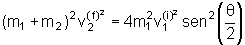
segue
que
|
|
|