|
A despeito de ser muito difícil, em geral, determinar a posição
e a velocidade de qualquer uma das partículas do sistema (tendo
em vista a dificuldade de encontrarmos a solução exata
para o sistema de equações ( )) existe um ponto no sistema
de partículas cujo movimento em um bom número de casos
é previsível. Esse ponto é o centro de massa.
O centro de massa é definido pelas suas coordenadas Rx,
Ry, e Rz
dadas pelas expressões:
 ,
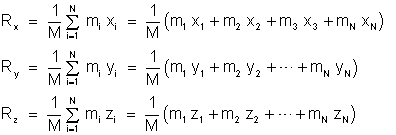onde m de M é
a massa total do sistema de partículas
 .
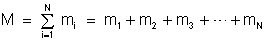Podemos assim escrever, vetorialmente, que o vetor de posição
do centro de massa ( )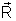
é dado por
 .
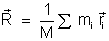No caso de um sistema composto por um número muito grande de
partículas é preferível tratá-lo como
uma distribuição contínua de partículas
e não discreta. Nesse caso, um dos conceitos mais relevantes
é a densidade. A densidade de massa é definida como
a relação entre a quantidade de massa dm contida num
elemento infinitesimal de volume dV. Definimos, portanto
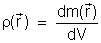
onde
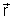é o vetor posição do elemento de volume dV.
Dada a densidade volumétrica de massa podemos calcular a massa
total através da integral de volume da densidade
 .
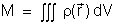Para uma distribuição contínua de massa o centro
de massa é dado por
 .
|
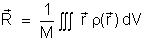