Consideremos o movimento de um mesmo objeto analisado de dois sistemas de coordenadas (S e S') diferentes. Supomos que S' realiza um movimento de translação com respeito a S, isto é, os seus eixos permanecem paralelos aos de S (por exemplo, como na figura anterior) e esteja dotado de uma aceleração em relação a S.

No sistema S escrevemos

.

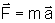
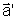A relação entre as acelerações num sistema () e no outro () é

.

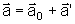
Portanto, podemos escrever

.

Vemos assim que a força de inércia no sistema acelerado é

.

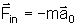
Para entendermos melhor o que foi dito, vamos estudar um caso concreto. Consideremos um elevador em queda livre dentro do qual uma pessoa abandona um livro.

Analisemos o movimento do livro visto da Terra e do elevador. O elevador está acelerado em relação à Terra (neste caso, com aceleração ).

Visto da Terra escrevemos, para o movimento (aceleração) do livro,

.

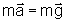
ou seja, o livro está acelerado com aceleração .

Visto do elevador, a situação é muito diferente. O passageiro verá o livro flutuar (essa situação é às vezes descrita como zero g). O livro estará em repouso em relação do elevador. O passageiro escreverá simplesmente

.

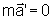
Como é possível a aceleração ser nula no sistema do elevador?

Já vimos que no sistema não-inercial (acelerado) surge a força de inércia

.

Portanto, a equação correta para o astronauta é

demonstrando, assim, que as descrições são absolutamente coerentes e compatíveis entre si.

Gil Marques