 .
.
ENERGIA DO MOVIMENTO HARMÔNICO SIMPLES
Já vimos no curso de Mecânica que a energia potencial associada a uma força elástica é dada por
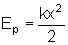 .
.
Utilizando
a expressão x(t) = A cos(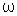 t
+
t
+ 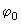 )
vemos que a energia potencial varia com o tempo de acordo com a expressão
)
vemos que a energia potencial varia com o tempo de acordo com a expressão
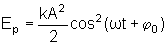 .
. A energia cinética, dada por
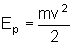 ,
, também
varia com o tempo. Utilizando v(t) = -A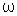 sen(
sen(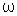 t
+
t
+ 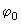 )
vemos que a dependência da energia cinética com o tempo é
dada por
)
vemos que a dependência da energia cinética com o tempo é
dada por
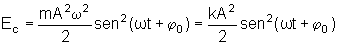 .
. onde, na
expressão acima utilizamos a relação 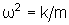 .
.
A soma da energia cinética com a energia potencial nos dá a energia
mecânica (E). Nesse caso escrevemos
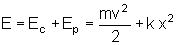 .
. Sabemos
que a energia mecânica se conserva no movimento. Podemos verificar isso
explicitamente somando as expressões 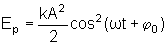 e
e 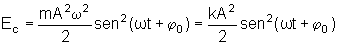 .
Obtemos
.
Obtemos
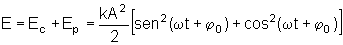 .
. Sabemos que
 .
Portanto, segue de
.
Portanto, segue de
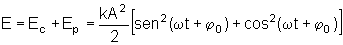
que a expressão da energia mecânica é:
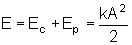 .
. A figura abaixo ilustra o que acontece com as várias formas de energia, à medida em que o tempo passa.
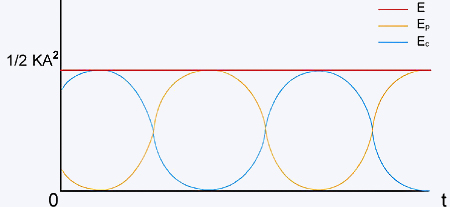
Note-se que a energia cinética e a energia potencial variam de tal forma que a soma permanece constante.