|
O
movimento oscilatório, bastante comum no cotidiano, é
um caso especial de movimento periódico. Dizemos que o movimento
periódico é oscilatório (usa-se também
vibratório) se o sentido do movimento é invertido regularmente.
Entende-se aqui por inversão a mudança de sentido da
velocidade.
| O
movimento do pêndulo simples nos proporciona o exemplo
mais simples de movimento oscilatório. Outro exemplo
é aquele do movimento de uma partícula presa a
uma mola. As cordas de um violão executam, igualmente,
movimentos oscilatórios, assim como as hastes de um diapasão.
|
|
Os movimentos oscilatórios são tais que as equações
horárias desses movimentos podem ser expressas em funções
seno e cosseno. Como essas funções (seno e cosseno)
são também designadas por funções harmônicas
é comum nos referirmos aos movimentos oscilatórios como
movimentos harmônicos. Quando podemos utilizar apenas uma função
seno (ou cosseno) para a equação horária do movimento,
dizemos que o movimento harmônico é
simples (ou apenas Movimento Harmônico Simples).
Num movimento harmônico simples ao longo de um eixo, digamos
x, a coordenada x depende do tempo da seguinte forma:
.
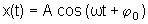Observe-se
que essa expressão segue da própria definição
de movimento harmônico simples.
Na
expressão acima a constante A recebe o nome de amplitude
do movimento. Tal nome decorre do fato de esse valor ser aquele
para o qual a variável x tem o valor máximo
(ou o mínimo). Isto se pode ver a partir do gráfico
de x x t.
O
valor constante
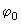é denominado de constante de fase ou fase
inicial.
Denominamos
o termo
de fase
do movimento harmônico simples.
|
|
Observe-se
que o movimento harmônico simples se repete sempre que a fase
é acrescida de um valor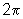 
radianos. Isto nos permite determinar o período (T) do movimento.
Pois quando a fase é acrescida de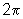
radianos o tempo passou de t para t + T. Podemos assim escrever
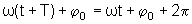
de
onde resulta
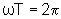
e,
portanto,
.
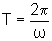A
freqüência f é, pois,
.
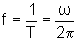
A
constante
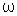é denominada freqüência angular e, em termos da
freqüência e do período ela é dada por
.
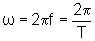Unidade
do período: O período tem a mesma unidade que o
tempo (segundo, minuto, hora).
Unidade
de freqüência: A freqüência (f) mede o número
de repetições por unidade de tempo. Suas unidades são:
Hertz
(Hz) - ciclos por segundo
r.p.m. - rotação por minuto
r.p.s. - rotação por segundo
etc.
| EXPRESSÕES
PARA VELOCIDADE E A ACELERAÇÃO NO MOVIMENTO HARMÔNICO
SIMPLES |
|
| FORÇAS
QUE PRODUZEM O MHS |
|
| ENERGIA
DO MOVIMENTO HARMÔNICO SIMPLES |
|
Gil
Marques
|
