Podemos introduzir dois tipos de produtos entre vetores.

O primeiro produto é conhecido como produto escalar de dois vetores. Esse nome decorre do fato de o resultado desse produto ser uma grandeza escalar.

O segundo é o produto vetorial. Neste caso, o resultado do produto é um outro vetor.

Sejam dois vetores e . O produto escalar dos vetores e , que representamos por é definido como sendo dado pelo produto dos módulos de cada um dos vetores multiplicado pelo coseno do ângulo formado pelos dois vetores: . Uma outra definição, inteiramente equivalente, é em termos das componentes dos vetores: .

Consideremos dois vetores e . O produto vetorial de dois vetores, representado por 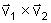, é um vetor indicado com

,

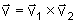cujas características são:

a) Direção - do eixo perpendicular ao plano formado pelos vetores e .

b) Sentido - para determinar o sentido, use sua mão direita (essa regra é conhecida como regra da mão direita). Com os dedos da mão procure levar o vetor para o vetor . O sentido será dado pelo polegar da mão direita.

c) Módulo - O módulo de v é dado pela expressão

,

ou seja, o módulo de é dado pelo produto dos módulos vezes o seno do ângulo entre os dois vetores.

Gil Marques