| |

| Em medidas físicas é facil
encontrar uma dispersão de valores muito grande. O
raio de um átomo e o raio de um universo é só
um exemplo entre tantos. Para expressar esses valores adequadamente,
é conveniente o uso da notação científica.
Escreve-se o valor com apenas um dígito antes
da vírgula, completa-se com algarismos decimais
necessários (eventualmente truncando e arredondando
o valor em alguma casa decimal) e se multiplica tudo pela
potência de dez adequada. |
|
Por exemplo, o comprimento de um fio vale
14269513 mm ou é da ordem de 1,43x107 mm. Note
que se usaram apenas dois algarismos após a vírgula
sendo que o último foi arredondado para “cima”
uma vez que 1,4269 está mais próximo de 1,43 que de
1,42. A regra de arredondamento aqui proposta é a de arredondar
o último dígito para “cima” caso o próximo
dígito seja
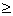 5, mantendo-o caso contrário.
Note que ao truncar e arredondar as casas decimais, perdemos muito
da informação inicial, mas isso pode ser remediado
usando quantos algarismos forem necessários depois da vírgula,
como por exemplo, 1,4269513 x 107 mm reproduz o valor
com toda a precisão inicial.
5, mantendo-o caso contrário.
Note que ao truncar e arredondar as casas decimais, perdemos muito
da informação inicial, mas isso pode ser remediado
usando quantos algarismos forem necessários depois da vírgula,
como por exemplo, 1,4269513 x 107 mm reproduz o valor
com toda a precisão inicial.
Existem outras regras de arrendodamentos,
mais complicadas, um pouco mais precisas mas nenhuma é exata.
A regra aqui proposta é também adotada pela maioria
das calculadoras e algoritmos em computadores.
Denomina-se algarismo significativo o número
de algarismos que compõe o valor de uma grandeza, excluindo
eventuais os zeros à esquerda usados para acerto de
unidades. Mas atenção: ZEROS À DIREITA SÃO
SIGNIFICATIVOS. Na tabela a seguir um mesmo valor do raio de uma roda
é escrito com diferente número de algarismos significativos.
|
raio (mm) |
significativos |
| 57,896 |
5 |
| 5,79x101 |
3 |
| 5,789600x101 |
7 |
| 0,6x102 |
1 |
A
escolha de quantos significativos serão usados no valor da
grandeza depende da grandeza, do processo de medida e do instrumento
utilizado.
O
NÚMERO DE ALGARISMOS SIGNIFICATIVOS DE UMA
GRANDEZA É DETERMINADO PELA SUA INCERTEZA
|

Para
a expressão da incerteza adaptaremos a convenção
sugerida por Vuolo (1992).
Um
outro exemplo é ilustrado a seguir: Suponha que se deseje
medir o tamanho do besouro.
| |
Uma vez decidido o que caracteriza o tamanho
do besouro, qual das alternativas abaixo melhor caracteriza
a medida do tamanho do besouro?
a) Entre
0 e 1 cm
b) Entre 1 e 2 cm
c) Entre 1,5 e 1,6 cm
d) Entre 1,54 e 1,56 cm
e) Entre 1,546 e 1,547 cm |
Acertou quem optou pela alternativa d).
Isso porque, na leitura de uma escala, o algarismo significativo mais
à direita de um número deve sempre ser o duvidoso (não
esqueça: o algarismo duvidoso é significativo!). Resumindo:
Qualquer medida por comparação entre um objeto e uma
escala deve incluir além dos dígitos exatos (1,5 nesse
caso) uma estimativa do dígito (duvidoso). Uma vez que a régua
foi marcada em milímetros você deve estimar o comprimento
fracionário (em décimos de mm) que melhor expressa a
medida. Você pode não precisar se vale 1,54, 1,55 ou
mesmo 1,56. Essa é a expressão da sua incerteza.
| |
Só para confirmar: Qual o diâmetro
da moeda?
a) Entre 0 e 2 cm
b) Entre 1 e 2 cm
c) Entre 1,9 e 2,0 cm
d) Entre 1,92 e 1,94 cm
e) Entre 1,935 e 1,945 cm |
No exemplo acima podemos afirmar que a metade
da menor divisão é uma estimativa da nossa incerteza:
portanto o diâmetro da moeda pode ser expresso como:
1,92 ± 0,05 cm
1,92(5) cm

Como
devemos expressar a incerteza de uma medida? Ou, posto de outra forma:
quantos significativos devem ter a incerteza de uma medida? Usaremos a seguinte convenção:
Conforme Vuolo (1992) e Inmetro
(1998).
-
Se o primeiro dígito significativo
da incerteza for menor que 3, usaremos DOIS significativos.
-
Caso o primeiro dígito significativo
da incerteza for maior ou igual a 3, podemos usar UM ou DOIS algarismos
significativos para a incerteza;
| Resumindo: |
| Qualquer que seja o caso sempre podemos usar
dois significativos para expressar a incerteza. Mas atenção:
quando a incerteza for resultado de uma estimativa ou apenas
indicativa, tal como a metade da menor divisão de um
instrumento, sugerimos usar apenas UM dígito significativo.
Não tem sentido, por exemplo, expressar a incerteza
de uma régua milimetrada com DOIS significativos (0,50mm),
basta escrever 0,5mm. |

- Usar a mesma potência de dez tanto para o
valor da grandeza como para sua incerteza;
- O número de algarismos significativos da incerteza é
dado pela regra 1.2.1. acima;
- O número de dígitos depois da vírgula na incerteza
tem que ser o mesmo que no mensurando;
- A notação científica pode ser usada para melhor
legibilidade.
Veja
alguns exemplos abaixo. Note o casamento do número de casas
decimais na incerteza e no valor do mensurando.
|
notação errada |
notação correta |
| 5,30 ± 0,0572 |
5,30 ± 0,06 |
| 124,5 ± 11 |
125 ± 11 |
| 0,0000200 ± 0,0000005 |
(200,0 ± 5,0)x10-7 |
| (45 ± 2,6)x101 |
(45 ± 3) x 101 |
Manfredo H. Tabacniks
|
|