| Objetivos: |
1.
Observar e analisar o movimento oscilatório de um sistema
massa-mola.
2. Medir períodos de oscilação.
3. Verificar a dependência do período do movimento com a massa
acoplada (m) e com a dureza da mola (k). |
| Introdução:
O período de oscilação de um sistema massa-mola como o da
figura abaixo é dado pela relação
 ,
onde
é a freqüência angular do movimento oscilatório.
Supondo-se
a massa da mola desprezível frente à da massa m acoplada,
o período pode ser escrito como
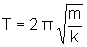
onde
k é o coeficiente de restituição da mola.
|
|
| Material
necessário: |
molas
com diferentes coeficientes de restituição (k);
massas diferentes (blocos de madeira ou argolas metálicas). |
Procedimento:
1.
Monte o sistema massa e mola, como mostra a figura.
2. Meça, com o auxílio de massas diferentes e conhecidas (m), a constante
k da mola, lembrando que F = -kx, onde x é a distensão da mola e P
= mg.
3.
Acople agora uma massa M1 e faça
o sistema oscilar de forma uniforme (sem deixar dar pinotes!) Meça
o intervalo de tempo de 5 oscilações (ou mais) e obtenha o período.
Repita a medição várias vezes, organize uma tabela. Meça a massa M1
numa balança.
Lembre-se
de que o desvio
é dado pelo (valor máximo - valor mínimo)/2.
4. Utilize os valores obtidos para k e M1
e calcule o período esperado através da relação
.
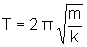Compare com o valor experimental.
5.
Acople agora 2 blocos, repita as medições do período e estenda a tabela
iniciada anteriormente. Faça ainda para 3 blocos, se a mola for adequada,
e estenda a tabela anterior. Calcule os valores esperados e compare
com as medidas de períodos para cada caso.
6.
Agora use apenas 1 bloco e repita o procedimento para outras molas
(diferentes valores de k). Meça os períodos e compare com os valores
esperados.
Observação:
Grupos diferentes de alunos poderiam usar molas diferentes e, ao
juntar as informações de toda a classe, seriam obtidos os mesmos
resultados sem tanta repetição!
| Objetivos: |
1.
Usar um sistema massa-mola para medir aceleração.
2. Uso da segunda lei de Newton. |
Introdução:
Como
já foi visto, a força elástica que age na mola é dada pela relação
F = -kx. Uma vez distendida a mola, se acoplamos uma massa M na sua
extremidade, ela será acelerada. Conforme a 2ª lei de Newton F = Ma,
a aceleração alcançada depende da massa. Supondo-se o atrito desprezível,
aumentando-se a massa, a aceleração deve diminuir para uma dada força
aplicada.
| Material
necessário: |
Use
uma mola conhecida, agora montada na horizontal, sobre uma placa
lisa de madeira ou de plástico, como indicado abaixo. |
Procedimento:
1.
Monte um sistema semelhante ao mostrado acima e estude qualitativamente
o movimento, com diferentes distensões e diferentes massas.
2. Meça a massa M.
3. Escolha o intervalo adequado de distensão, para a massa escolhida,
meça a aceleração para diferentes valores de distensão x. Como k já
é conhecido,
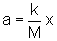
4.
Aumente a massa e obtenha novamente as acelerações.
1) Cole duas réguas sobre uma mesa para servir de trilha para um carrinho.
Nas extremidades das réguas cole um elástico, como mostra a figura.
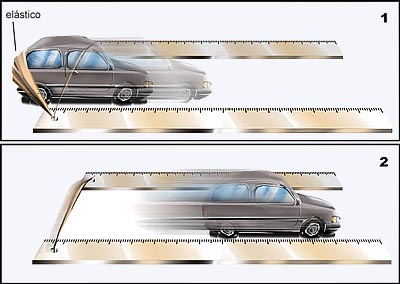
Empurre o carrinho para trás, esticando um pouco o elástico, e solte-o
Observe onde ele pára. Empurre o carrinho mais para trás, forçando
o elástico a se esticar mais que na etapa anterior. Solte-o e observe
onde o carrinho pára.
Discuta o que aconteceu.
2) Em vários alunos, tente seguir uma "bolinha maluca" que pula. Ela
deve pular cada vez menos. Tente medir aproximadamente as alturas
máximas alcançadas pela bolinha.
Discuta o que foi observado.
3)
Tente estudar como funciona o sistema amortecedor de um automóvel.
4) Use uma mola grande e estude o comportamento.
Marques e Ueta
