Quando um objeto fica sujeito a uma força elástica, o seu movimento recebe o nome de movimento harmônico simples.

Uma das características desse movimento é que ele é periódico. Isso ocorre porque a partícula (desprezando o atrito) volta a uma certa posição a intervalos de tempo regulares. Esse intervalo de tempo é o período. Por exemplo, você perceberá que a partícula passará pelo centro na mesma direção a intervalos regulares (o período de tempo).

O período se relaciona com a massa e a constante elástica. Verifica-se que o período é dado pela expressão

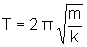
onde m é a massa da partícula. Assim, como é fácil determinar a massa de uma partícula, pode-se determinar k a partir do período.

Outra coisa interessante a respeito do movimento é que, devido à força ser elástica, a partícula atinge uma certa distância máxima da origem e depois volta. Esse deslocamento máximo é conhecido como amplitude.

Nota-se também que, nos pontos de maior velocidade, o deslocamento é pequeno e, onde o deslocamento é grande, a velocidade é pequena. Por exemplo, na origem (deslocamento igual a zero x = 0), a velocidade é máxima. Quando o deslocamento é máximo (atinge sua amplitude), a velocidade é nula (a partícula está instantaneamente em repouso).

Pode-se verificar que, no movimento harmônico simples, vale o seguinte resultado:

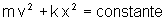
ou seja, a massa vezes a velocidade ao quadrado, quando adicionado ao produto de k vezes x2, é o mesmo em qualquer ponto onde a mola estiver. Veremos, depois, que a constante é igual a duas vezes o valor da energia no movimento harmônico simples. Isto é,

constante = 2Energia

Finalmente, usando a lei de Newton, podemos relacionar, para cada deslocamento x, o valor da aceleração. Tem-se que

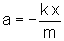
Marques e Ueta