Objetivos:

1. Utilizar a 2ª lei de Newton. 2. Comparar a aceleração obtida através da 2ª lei de Newton com a obtida cinematicamente.

 

 

Material: carrinho, tábua ou trilho, blocos de madeira, cronômetro.

Arranjo experimental:

Use uma tábua lisa (ou um trilho) de aproximadamente 1 metro de comprimento como um plano inclinado, apoiando uma das extremidades em blocos de madeira.

Escolha um carrinho que deslize livremente pelo plano inclinado. Admitindo que praticamente não há atrito entre o carrinho e o plano, a única força responsável pela descida do carrinho (de massa m) é a força peso .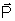

A projeção dessa força na direção do movimento é 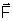, cujo módulo , onde 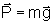. A força 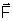tem a direção e o sentido do movimento, como mostra a figura. 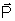e 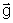têm a direção vertical e sentido para baixo.

Em São Paulo, g = 9,8 m/s².

A aceleração a do carrinho de massa m é dada por

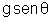
Procedimento:

1. Meça o ângulo q com o auxílio de um transferidor ou através de relações trigonométricas no triângulo.
2. Calcule a aceleração do carrinho .
3. Marque uma posição da rampa com um traço. Solte o carrinho desse ponto, com velocidade inicial nula. Alinhe a parte frontal do carrinho com o traço e use a parte frontal como referência. (Para facilitar, você pode usar algum outro ponto mais definido do carrinho como referência.)
4. Cronometre o intervalo de tempo de descida t. Use a parte frontal do carrinho (ou outro ponto escolhido), observando o movimento numa posição adequada para evitar erros. Se for possível, observe bem por cima. Organize os dados em uma tabela.
5. Calcule o valor médio do tempo de descida t e o respectivo desvio.
6. Obtenha a aceleração a, lembrando que s = 1/2 at². Utilize os valores extremos de t, isto é, t + e t - , para obter os valores extremos de a, a_min e a_max, respectivamente. O desvio em a, deve ser obtido por:

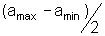
7. Compare 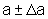com 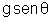. Discuta o resultado.
8. Se for colocado um peso adicional sobre o carrinho, o que acontece com a aceleração? Discuta e observe.

Observações: 1. Estamos admitindo que o ângulo pode ser obtido com precisão bem melhor que o tempo de descida t do carrinho. O tempo de reação do observador pode ter uma dispersão grande e afetar a medida t. Use trechos grandes e inclinações pequenas para aumentar o intervalo de tempo de descida. 2. O desvio em pode ser obtido da seguinte forma, uma vez que seja feita a estimativa de desvio em . Dado , o ângulo é no máximo e, no mínimo, . Calcule gsen() e g.sin(), que são, respectivamente, o valor máximo e o mínimo da aceleração. O desvio é obtido pela metade da diferença entre esses valores extremos.

1) Carro sem partida.

Se apenas uma pessoa empurrar um carro sem partida para fazê-lo pegar no arranque, numa rua plana, dificilmente conseguirá a aceleração necessária. Entretanto, se três ou quatro pessoas empurrarem simultaneamente, o carro adquirirá a aceleração suficiente para conseguir o arranque. Uma força maior aplicada sobre a mesma massa resultará numa aceleração proporcionalmente maior.

2) Dois carros enguiçados.

Se agora tiver um carro leve e outro bem pesado para empurrar, certamente é mais fácil mover o carro mais leve. A massa maior é mais difícil de ser acelerada.

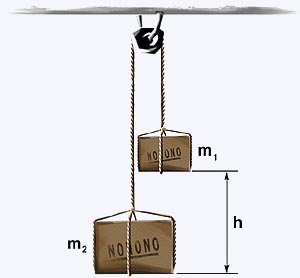
3) Dois objetos ligados por um fio. Tome dois objetos de massas diferentes m1 e m2, presos a um fio e acoplados a uma roldana, como mostra a figura. Utilize a 2ª lei de Newton e determine a aceleração do conjunto quando soltamos as duas massas. Determine o tempo necessário para atingirem a mesa quando soltos de uma altura H. Se m1 >> m2, o que se espera? Se as massas m1e m2 forem iguais e se uma delas for deslocada um pouco da posição inicial, o que acontece? Você vê algum uso prático para um sistema semelhante?

4) Massas sobre uma mesa.

Faça a montagem ilustrada na figura. Inicialmente faça previsões do que vai ocorrer, apenas com as massas m₁ e M (m₁< M). Utilize blocos de madeira ou caixas lisas de papelão, observe e confira com as previsões. Coloque a massa m₂ sobre a m₁ e repita o procedimento.

Marques e Ueta