A extensão do movimento harmônico simples para o caso bidimensional é a seguinte: considere-se o caso de uma força tal que para suas componentes x e y podemos escrever:

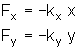
As equações de movimento agora são:

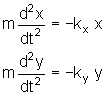
Definindo as freqüências angulares

As soluções para as componentes x e y do vetor posição são:

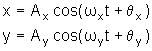
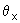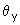onde A_x e A_y são as amplitudes nas direções x e y e e suas respectivas fases.
O movimento harmônico simples resultante da composição dos dois movimentos (no eixo x e eixo y) pode ser analisado em função das freqüências e fases. O movimento resultante terá lugar numa região do espaço que é um retângulo de lados 2A_x e 2A_y.
Se as freqüências angulares 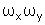forem comensuráveis, isto é, se houver algum conjunto de números inteiros tais que

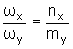
Então a trajetória será uma curva fechada e o movimento será periódico. O período será dado por

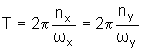
Durante um período T a coordenada x executa n_x oscilações e a coordenada y executa n_y oscilações.
Se e são comensuráveis, então, em função das fases e podemos obter figuras muito interessantes. Essas figuras são conhecidas como figuras de Lissajoux.
Figuras análogas às de Lissajoux podem ser obtidas num osciloscópio de raios catódicos aplicando ao feixe voltagens oscilantes de uma forma conveniente.
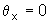Se e 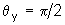obtemos uma circunferência ?? como trajetória.