Para encontrarmos a transformação que nos leva de um conjunto de coordenadas de um evento (x, y, z, t) para outro (x', y', z', t')

(x, y, z, t) ® (x', y', z', t')

O fato de que essas transformações devem ser lineares decorre do seguinte:

1. Como o movimento do sistema B é retilíneo e uniforme, o movimento do sistema A (em relação a B) também é um movimento retilíneo e uniforme.
2. Para V = 0 a transformação se reduz à identidade.
3. Como a frente onda de um sinal luminoso se propaga com a mesma velocidade c, então se ele é enviado quando as origens coincidem e com t = t'= 0, podemos escrever para ela que:

x² + y² + z² - c²t² = 0

x'² + y'² + z'² - c²t'² = 0

Pode-se mostrar que a transformação linear mais geral, obedecendo a esses critérios, é a transformação de Lorentz especial:

	(1)
	(2)
y' = y	(3)
z' = z	(4)

As transformações inversas são:

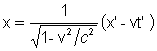
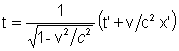
y = y'

Como era de se esperar, essas últimas são obtidas das anteriores pela substituição

v ® -v

Finalmente, podemos ver que, para fenômenos tais que

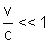
Podemos escrever, dentro de uma boa aproximação, utilizando as equações (1), (2), (3) e (4):

x'= x - vt

t'= t

y'= y

z'= z

Estas transformações são exatamente as transformações de Galileu. As transformações de Galileu são válidas como uma aproximação. No cotidiano é difícil perceber uma distinção entre elas. Isso explica por que só neste século viemos a nos dar conta de que as transformações de Galileu não são exatas.

Por exemplo, para um avião a jato que se move a 1080km/h (300m/s), v/c tem o valor

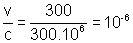
A alteração dos resultados são, portanto, imperceptíveis no nosso cotidiano.