A 2a
lei elementar de Laplace diz que o módulo da força
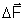 que atua em
que atua em
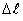 vale:
vale:

Isto é, a
força que atua no elemento de condutor é diretamente proporcional
à intensidade da corrente, à indução magnética, ao comprimento
do elemento e ao seno do ângulo que o elemento faz com a indução
magnética. Essa é a 2a lei elementar de Laplace.
A força
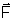 que atua no condutor inteiro é dada pela soma vetorial
de todos êsses
que atua no condutor inteiro é dada pela soma vetorial
de todos êsses
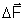 .
.

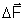 é perpendicular ao plano determinado por
é perpendicular ao plano determinado por
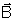 e
e
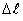 . No caso da figura 288, o plano determinado por
. No caso da figura 288, o plano determinado por
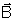 e
e
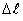 é o próprio plano do papel; então
é o próprio plano do papel; então
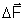 é perpendicular ao plano do papel.
é perpendicular ao plano do papel.

É
dado por uma regra prática, chamada regra dos três dedos
da mão esquerda: colocando-se o polegar no sentido do
campo e o indicador no sentido da corrente, então o médio
dará o sentido da força (fig. 289). Êsses três dedos devem ser da
mão esquerda. Na figura anterior, por exemplo,
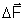 é dirigida para trás do papel.
é dirigida para trás do papel.
NOTA
IMPORTANTE
É
muito importante comparar o comportamento de um
campo magnético em relação a um ímã com o comportamento
em relação a uma corrente elétrica. Quando um ímã
é colocado num campo magnético, a força que atua
na massa magnética é dada por:
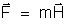 |
|
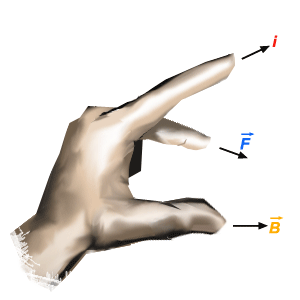 Figura 289 Figura 289 |
Quando uma
corrente elétrica é colocada em um campo magnético, a força que
atua num elemento
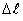 do condutor vale:
do condutor vale:
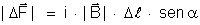
Portanto,
a intensidade de campo magnético,
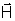 , é responsável pela força que atua numa massa magnética
(num ímã); a indução magnética,
, é responsável pela força que atua numa massa magnética
(num ímã); a indução magnética,
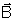 , é responsável pela força que atua numa corrente elétrica
(num condutor).
, é responsável pela força que atua numa corrente elétrica
(num condutor).

Poderá ocorrer
ao leitor a seguinte dúvida: como se deduzem as duas leis elementares
de Laplace?
Essas duas
leis não têm demonstração. Elas são na verdade dois postulados;
isto é, nós admitimos, como ponto de partida para o estudo dos
dois primeiros fenômenos eletromagnéticos, que as duas equações
de Laplace sejam verdadeiras, sem demonstrá-las diretamente.
E sabemos que elas realmente são verdadeiras porque as aplicações
dessas duas leis elementares sempre nos levam a resultados que
são confirmados pela experiência.