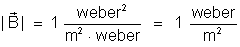Além do vetor
campo magnético
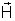, existe no campo magnético uma outra grandeza vetorial,
que desempenha papel importantíssimo em muitos fenômenos eletromagnéticos.
É chamada indução magnética, ou densidade de fluxo magnético e representada
por
.
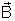| Chama-se
indução magnética em um ponto ao produto da permeabilidade magnética
do meio pelo campo magnético nesse ponto. Isto
é,
|
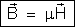
A direção e
o sentido da indução são a própria direção e sentido do campo magnético
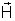. O módulo é igual ao produto de
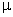pelo módulo de
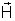, isto é,
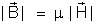
Admitindo-se
que o campo seja produzido por uma massa magnética puntiforme, o
módulo de
é:
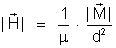
Logo
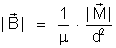
ou
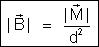
Concluímos que,
quando o campo magnético É PRODUZIDO POR UM ÍMÃ, a indução
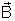num ponto depende exclusivamente da massa magnética que
produz o campo e da distância do ponto à massa magnética, MAS NÃO
DEPENDE DO MEIO.
Unidades
de indução magnética
A unidade de
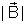é obtida considerando-se:
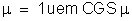(portanto, vácuo)
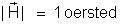
Resulta:
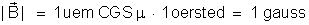
Um gauss é a
indução magnética num ponto de um campo magnético no vácuo no qual
a intensidade do campo é um oersted.
1a) Pelo
fato de ser
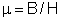é que a unidade de permeabilidade magnética do CGSEM
também é chamada gauss/oersted, conforme vimos no tópico
"Sistema de Unidades de Magnetismo e Eletromagnetismo"
.
2a) É
fácil provar que a indução magnética,
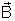, é grandeza física da mesma espécie que a intensidade
de imantação,
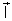, temos:
ou,
ou
|
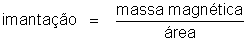
Indução e imantação
representam ambas o quociente de uma massa magnética por uma área
(ou quadrado de um comprimento, que é o mesmo). Esse é o motivo
pelo qual essas duas grandezas são avaliadas nas mesmas unidades.
No no tópico "Densidade
Magnética" provamos que densidade magnética é grandeza da mesma espécie que
a imantação, e que por isso também tem a mesma unidade que esta.
Na verdade, o nome gauss originalmente foi dado à unidade de
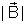, e depois passou a ser usado nas outras.
A unidade de
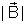é deduzida considerando-se:
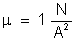(ver tópico "Sistema
de Unidades de Magnetismo e Eletromagnetismo")
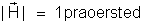
Resulta:
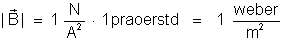
A unidade de
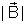no sistema MKS é chamada
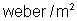, é a indução magnética num ponto de um campo magnético em
que a intensidade do campo é um praoersted, num meio em que a permeabilidade
magnética é
.
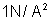Podemos concluir
que o produto de
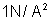por um praoersted dá
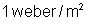, do seguinte modo: já vimos, que
.
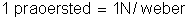Então:
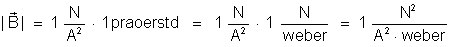
Considerando
a fórmula de Coulomb,
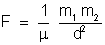
e escrevendo
as unidades das grandezas, temos:
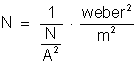
de onde tiramos
que:
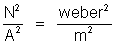
Então:
