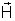é o quociente de uma força por uma massa magnética.

No cálculo do módulo suporemos que a massa magnética M que produz o campo seja puntiforme.  Repetindo o raciocínio desenvolvido no tópico "Características do Vetor Campo" para o caso do campo elétrico podemos provar que, sendo d a distância da massa magnética M ao ponto A, o módulo do campo magnético em A é

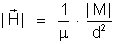
onde 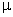 é a permeabilidade magnética do meio em que se produz o campo.

O campo magnético é também um campo newtoniano.  O vetor 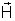 tem a direçao da reta MA.

Analogamente ao caso de campo elétrico, podemos provar que: quando M é positiva, isto é, é massa magnética de um polo norte, o senti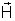do de  é o sentido MA; quando M é negativa, isto é, é massa magnética de um polo sul, o sentido de 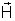 é o sentido AM (fig. 236).

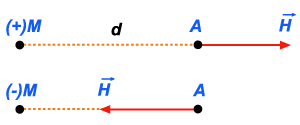
Figura 236

Recorde o tópico "Características do Vetor Campo" .

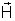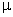Pelas características de  vemos que essa grandeza vetorial depende exclusivamente da massa magnética M, da permeabilidade  e da distância d.  E não depende da massa magnética m, que tínhamos suposto colocada em A para definirmos 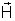.  Esse fato já está contido na definição de 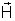, porque quando dizemos que o quociente 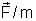 é constante, queremos dizer que ele não depende de 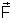 nem de m.