Vimos,
no tópico "Unidades
de Carga Elétrica" ,
que o sistema MKS contém unidades em toda a Eletricidade, isto é,
em Eletrostática, Eletrodinâmica, Magnetismo e Eletromagnetismo.
E que o sistema CGSES contém unidades só em Eletrostática e Eletrodinâmica.
Além
do CGSES, existe um outro sistema de unidades elétricas derivado
do CGS mecânico: é chamado CGS eletromagnético (abreviadamente,
CGSEM). Este sistema se inicia em Magnetismo, e é por isso que
somente agora vamos estudá-lo. Embora se chame CGS eletromagnético,
ele possui unidades também em Eletrostática e Eletrodinâmica, mas
nessas partes suas unidades não são usadas.

Recorde
o tópico "Unidades
de Carga Elétrica". Já dissemos que não
é possível construir-se um sistema de unidades elétricas partindo-se
exclusivamente das três unidades fundamentais da Mecânica, mas,
é necessário adotar-se uma quarta unidade fundamental, tipicamente
elétrica. Esta quarta unidade do sistema CGSEM é a de permeabilidade
magnética.
O
sistema CGSEM adota arbitrariamente o valor 1 para a permeabilidade
magnética do vácuo. A unidade de permeabilidade magnética deste
sistema se indica por
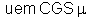 , ou
, ou
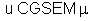 ; também é chamada gauss/oersted, por razões que veremos
mais tarde. (Tópico "Indução
Magnética ou Densidade de Fluxo Magnético")
; também é chamada gauss/oersted, por razões que veremos
mais tarde. (Tópico "Indução
Magnética ou Densidade de Fluxo Magnético")
As
unidades fundamentais do sistema CGSEM são, portanto:
1) unidade
de comprimento – centímetro
2) unidade de massa – grama
3) unidade de tempo – segundo
4) unidade de permeabilidade magnética – gauss/oersted,
ou
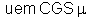 .
.

É
deduzida a partir da fórmula de Coulomb:
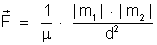
Considerando-se:
 Resulta:
Resulta:
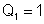 e
e
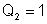
Portanto:
a unidade de massa magnética do sistema CGSEM é a massa magnética
puntiforme, que, colocada no vácuo a um centímetro de outra massa
magnética puntiforme igual, exerce sobre ela a repulsão de um dine.
Nota: A
permeabilidade magnética do ar é muito próxima da do vácuo. Na
prática a consideramos também igual a 1 gauss/oersted.

| |
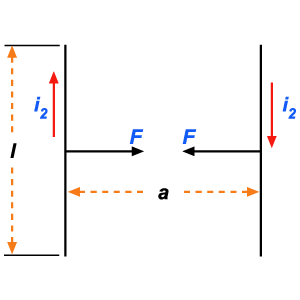 Figura 230 Figura 230 |
Vimos
que o ampère é definido do seguinte modo: ampère é a intensidade
de uma corrente invariável que, passando em dois condutores paralelos
e de comprimento infinito e distantes entre si de um metro, no vácuo,
faz aparecer em cada condutor a força de
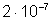 newtons por cada metro de condutor.
newtons por cada metro de condutor.

É
deduzida a partir da fórmula
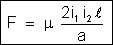 .
Tiramos:
.
Tiramos:

Se
fizermos:
 Resulta:
Resulta:
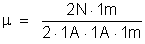
ou
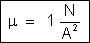
que
é a unidade de permeabilidade deste sistema.

É
calculada pela fórmula
 ,
bastando para isso colocar nessa fórmula os valores das grandezas
que entram na definição de ampère. Isto é, se considerarmos:
,
bastando para isso colocar nessa fórmula os valores das grandezas
que entram na definição de ampère. Isto é, se considerarmos:
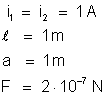
então
o
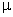 será o do vácuo. Representaremos por
será o do vácuo. Representaremos por
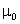 a permeabilidade do vácuo. Então:
a permeabilidade do vácuo. Então:
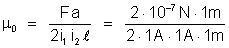
ou
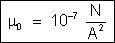
Nota: A
permeabilidade magnética do ar é muito próxima da permeabilidade
do vácuo. Na prática as consideramos iguais.

É
deduzida a partir da fórmula de Coulomb, considerando-se:

Resulta:
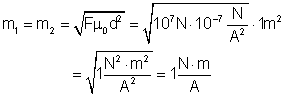
A
unidade de massa magnética do sistema MKS é a massa magnética puntiforme
que, colocada no vácuo a um metro de outra massa magnética puntiforme
igual exerce a repulsão de
 . É chamada
. É chamada
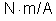 , e por razões que veremos mais adiante também é chamada
weber (tópico "Fluxo
Magnético num Campo Uniforme" ).
, e por razões que veremos mais adiante também é chamada
weber (tópico "Fluxo
Magnético num Campo Uniforme" ).