
Já
vimos que um ímã só possui propriedades magnéticas em certas regiões,
que chamamos regiões polares norte e sul, que elas possuem massas
magnéticas de iguais valores absolutos. Essas regiões polares de
um ímã não são pontos, mas são superfícies. As leis que estudamos
relativas à atração e repulsão, e a fórmula de Coulomb, só valem
para massas magnéticas puntiformes. Entretanto, no caso de um ímã
cujas massas magnéticas não são puntiformes também podemos aplicar
essas leis, pelo seguinte motivo: a massa magnética norte está distribuída
pela região polar norte. Mas, nessa região existe um ponto N tal
que, se a massa magnética estivesse concentrada nele, exerceria
o mesmo efeito que exerce quando está distribuída. Esse ponto N
é chamado polo norte. Do mesmo modo, polo sul é um ponto da região
polar sul tal que, se toda a massa magnética sul estivesse concentrada
nele, exerceria o mesmo efeito que quando está distribuída.
Desse
modo, trabalhando com polos, podemos aplicar a fórmula de Coulomb
e todas as consequências que resultarão dela. Por isso, daqui por
diante nos referiremos aos polos e não mais às regiões polares.
Chama-se
comprimento de um ímã à distância entre seus polos; representaremos
por
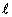 (fig. 228). (fig. 228).
|

Figuras 228
