
1. Calcular a
f.e.m. de um gerador de resistência
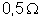 , sabendo que ele fornece corrente de 2 A para um circuito
de resistência
, sabendo que ele fornece corrente de 2 A para um circuito
de resistência
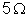 .
.
Para um circuito
fechado temos:
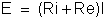
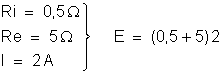 ou
ou
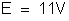
Resposta:
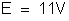 .
.
2. Um gerador
de f.e.m. 5 v e resistência interna
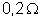 é ligado a um circuito de resistência
é ligado a um circuito de resistência
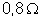 . Calcular a intensidade da corrente.
. Calcular a intensidade da corrente.
3. Calcular
a resistência interna de um gerador de f.e.m. 1,5 v, sabendo
que ligado a um circuito de
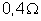 fornece corrente de 3 A.
fornece corrente de 3 A.
4. Um
gerador de f.e.m. 10 v e resistência interna
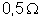 é ligado a um circuito de resistência
é ligado a um circuito de resistência
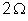 . Calcular: a) a intensidade da corrente; b) a
diferença de potencial entre os extremos do circuito externo;
c) a potência total que o gerador fornece; d) a
potência absorvida pelo circuito externo.
. Calcular: a) a intensidade da corrente; b) a
diferença de potencial entre os extremos do circuito externo;
c) a potência total que o gerador fornece; d) a
potência absorvida pelo circuito externo.

a) Temos:
|
 Figura 176 Figura 176 |
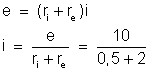
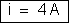
b) Sendo
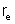 a resistência externa, i a intensidade da corrente, a diferença
de potencial entre os extremos do circuito externo é dada por
a resistência externa, i a intensidade da corrente, a diferença
de potencial entre os extremos do circuito externo é dada por
 ou
ou
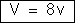
c) A potência
fornecida pelo gerador é:
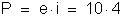
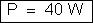
d) A potência
absorvida pelo circuito externo é:
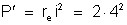
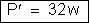
5. Um
gerador de f.e.m. e resistência interna constantes é ligado a um circuito
de resistência
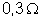 e fornece corrente constante de intensidade 5 A. Depois
é ligado a um circuito de resistência
e fornece corrente constante de intensidade 5 A. Depois
é ligado a um circuito de resistência
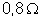 e fornece corrente constante de intensidade 2,5 A. Calcular
a resistência interna e a f.e.m. do gerador.
e fornece corrente constante de intensidade 2,5 A. Calcular
a resistência interna e a f.e.m. do gerador.
6. Um
gerador de resistência interna
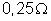 e f .e.m. 9 v é ligado a um circuito constituído por
três resistências ligadas em paralelo de valores
e f .e.m. 9 v é ligado a um circuito constituído por
três resistências ligadas em paralelo de valores
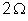 ,
,
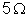 e
e
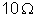 . Calcular: a) a resistência externa; b) a intensidade
da corrente que circula por cada resistência; c) a intensidade
da corrente total; d) a energia fornecida pelo gerador durante
meia hora; e) a energia absorvida pelo circuito externo durante
meia hora.
. Calcular: a) a resistência externa; b) a intensidade
da corrente que circula por cada resistência; c) a intensidade
da corrente total; d) a energia fornecida pelo gerador durante
meia hora; e) a energia absorvida pelo circuito externo durante
meia hora.

Figura 177

a) Cálculo
da resistência externa
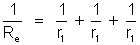
em que
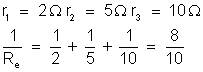
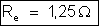
b) Cálculo
da intensidade total da corrente
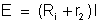 ou
ou
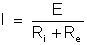
em que:
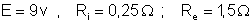
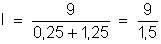 ou
ou
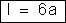
c) Corrente
nas derivações
Para isso temos
de calcular a diferença de potencial entre A e B. Temos:
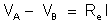
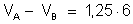 ou
ou
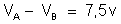
Aplicando a lei
de Ohm para cada derivação, temos:
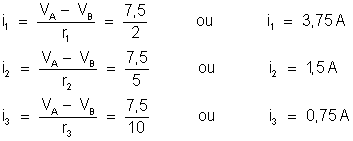
Verificação – Deve
ser verificada a igualdade:
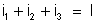
Com efeito,
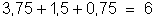
d) Energia
fornecida pelo gerador
Esta
energia vale:
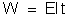
em
que

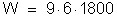 ou
ou
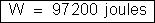
e) A
energia absorvida pelo circuito externo vale:
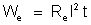
em que:

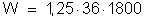 ou
ou
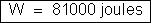
7. São
associados em série três geradores. Um tem f.e.m. de 2 v e resistência
interna de
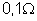 ; um outro tem f.e.m. de 3 v e resistência interna
; um outro tem f.e.m. de 3 v e resistência interna
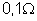 ; o terceiro tem f.e.m.de 5 v e resistência interna de
; o terceiro tem f.e.m.de 5 v e resistência interna de
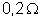 . Essa associação é ligada a três resistências conforme esquema
ao lado. Essas resistências valem respectivamente:
. Essa associação é ligada a três resistências conforme esquema
ao lado. Essas resistências valem respectivamente:
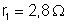 ;
;
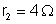 ;
;
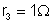 . Calcular: a) a resistência interna da associação;
b) a f.e.m. total da associação; c) a resistência externa;
d) a corrente
. Calcular: a) a resistência interna da associação;
b) a f.e.m. total da associação; c) a resistência externa;
d) a corrente
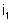 ; e) as correntes
; e) as correntes
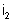 e
e
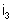 ; f) a energia fornecida pela associação durante 10 minutos;
g) a energia absorvida pelo circuito externo durante 10 minutos;
h) a energia absorvida pelas resistências
; f) a energia fornecida pela associação durante 10 minutos;
g) a energia absorvida pelo circuito externo durante 10 minutos;
h) a energia absorvida pelas resistências
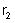 e
e
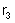 durante 10 minutos; i) a quantidade de calor que seria
libertada entre A e B se toda a energia elétrica absorvida nesse trecho
fosse transformada em calor.
durante 10 minutos; i) a quantidade de calor que seria
libertada entre A e B se toda a energia elétrica absorvida nesse trecho
fosse transformada em calor.
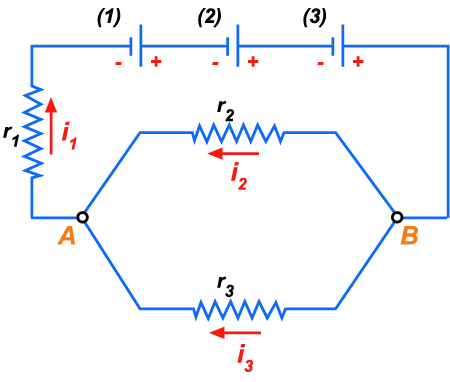
Figura 178

a) Resistência
interna da associação
Sendo
associação em série, a resistência. interna total é a soma das resistências
internas:
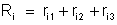
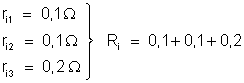 ou
ou

b) F.E.M.
da associação – Sendo associação em série, a
f.e.m. total é a soma das f.e.m.
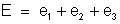
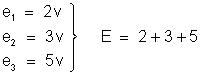 ou
ou
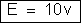
c) Resistência
externa – É
a soma da resistência
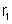 com a resistência do trecho AB, isto é,
com a resistência do trecho AB, isto é,
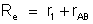
Temos:
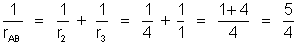
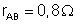 . Sendo
. Sendo
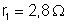 , temos:
, temos:
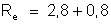 ou
ou
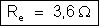
d) Corrente
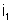 – No circuito dado, temos:
– No circuito dado, temos:
 ou
ou
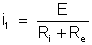
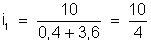 ou
ou
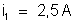
e) Correntes
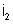 e
e
 – Para o cálculo destas correntes precisamos
calcular a diferença de potencial entre A e B. Temos:
– Para o cálculo destas correntes precisamos
calcular a diferença de potencial entre A e B. Temos:
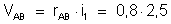 ou
ou
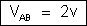
Aplicando
a lei de Ohm sucessivamente as resistências
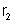 e
e
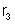 , temos:
, temos:
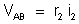 ou
ou
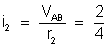 ou
ou
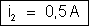
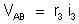 ou
ou
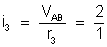 ou
ou
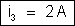
Verificação – Deve
ser satisfeita a igualdade
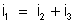
Com
efeito
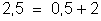
f) Energia
fornecida pela associação
A
energia fornecida pela associação vale:
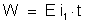
em
que:
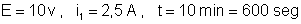
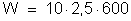 ou
ou

g) Energia
absorvida pelo circuito externo
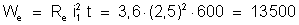

h) Energia
absorvida por
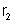 e
e
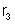
Vale:
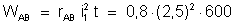

i) Quantidade
de calor libertado em AB
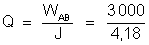
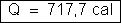
8. Três
pilhas de f.e.m. iguais de 1,5 v e resistências internas iguais
de
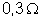 são ligadas em paralelo entre dois pontos M e N. O circuito
externo é constituído pelas resistências
são ligadas em paralelo entre dois pontos M e N. O circuito
externo é constituído pelas resistências
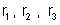 e
e
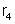 ligadas como mostra a figura 179, valendo respectivamente:
ligadas como mostra a figura 179, valendo respectivamente:
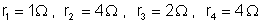 . Calcular: a) a intensidade da corrente que passa por
. Calcular: a) a intensidade da corrente que passa por
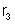 ; b) as intensidades das correntes que passam por
; b) as intensidades das correntes que passam por
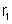 e
e
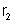 ; c) a potência fornecida pela associação; d) a
potência absorvida por
; c) a potência fornecida pela associação; d) a
potência absorvida por
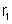 e
e
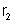 juntas.
juntas.
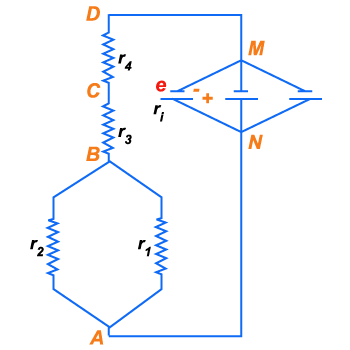
Figura 179
9. Dois
geradores idênticos (de mesma f.e.m. e mesma resistência interna)
de f.e.m. igual a 1,5 v e resistência interna
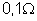 são ligados em paralelo. Três outros idênticos de f.e.m.
2 v e resistência interna
são ligados em paralelo. Três outros idênticos de f.e.m.
2 v e resistência interna
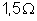 são ligados em paralelo. Cinco outros idênticos, de f.e.m.
3 v e resistência interna
são ligados em paralelo. Cinco outros idênticos, de f.e.m.
3 v e resistência interna
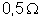 também ligados em paralelo. Depois as três associações em
paralelo são ligadas em série (fig. 180). Calcular: a) a
f.e.m. e a resistência interna da associação; b) a intensidade
da corrente que circula por uma resistência
também ligados em paralelo. Depois as três associações em
paralelo são ligadas em série (fig. 180). Calcular: a) a
f.e.m. e a resistência interna da associação; b) a intensidade
da corrente que circula por uma resistência
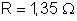 ligada aos terminais da associação; c) a quantidade
de calor libertada pela resistência R durante um minuto, se toda a
energia elétrica absorvida por R fosse transformada em calor.
ligada aos terminais da associação; c) a quantidade
de calor libertada pela resistência R durante um minuto, se toda a
energia elétrica absorvida por R fosse transformada em calor.
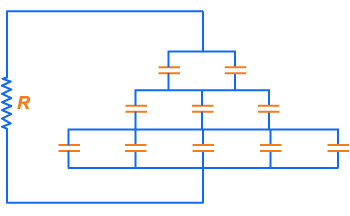
Figura 180
10. São
associados em série duas pilhas: uma de f.e.m. 2 v e resistência
interna
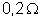 ; outra de f.e.m. 2,5 v e resistência interna
; outra de f.e.m. 2,5 v e resistência interna
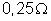 . A associação é ligada às resistências
. A associação é ligada às resistências
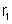 e
e
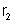 conforme o esquema. A resistência r vale
conforme o esquema. A resistência r vale
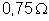 ;
;
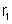 vale
vale
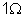 ;
;
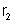 é um reostato que varia entre 0 e
é um reostato que varia entre 0 e
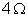 . Pergunta-se: 1) a diferença de potencial entre A e
B é maior quando
. Pergunta-se: 1) a diferença de potencial entre A e
B é maior quando
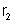 está fora do circuito, ou quando está intercalada no circuito?
2) as intensidades das correntes que passam por r,
está fora do circuito, ou quando está intercalada no circuito?
2) as intensidades das correntes que passam por r,
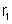 e
e
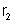 respectivamente, quando
respectivamente, quando
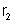 está intercalada no circuito?
está intercalada no circuito?
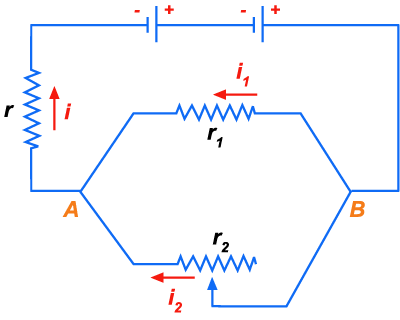
Figura 181
11. Duas
pilhas de f.e.m.
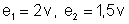 e resistências internas respectivas de
e resistências internas respectivas de
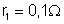 e
e
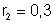 são ligadas em paralelo como mostra a figura 182.
Calcular as intensidades das correntes
são ligadas em paralelo como mostra a figura 182.
Calcular as intensidades das correntes
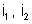 e i, sabendo que a resistência r vale
e i, sabendo que a resistência r vale
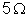 .
.
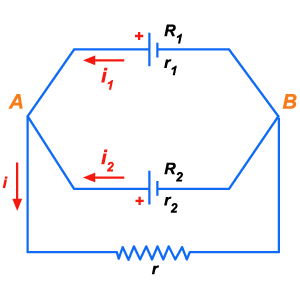
Figura 182
Solução:
Como se trata de duas pilhas diferentes ligadas em paralelo, o problema
deve ser resolvido pelas leis de Kirchhof'f. Havendo três incógnitas,
precisamos de três equações. Começamos atribuindo arbitrariamente
às correntes sentidos quaisquer, por exemplo, os sentidos indicados
na acima. A primeira lei de Kirchhoff pode ser aplicada
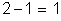 vez, porque há dois nós. Isto é,
vez, porque há dois nós. Isto é,
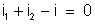
As
duas outras equações serão obtidas aplicando-se as duas malhas à segunda
lei de Kirchhoff. Percorramos a malha formada pelas duas pilhas no
sentido anti-horário e apliquemos a equação:

A f.e.m.
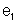 será tomada com o sinal
será tomada com o sinal 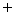 porque o sentido de percurso coincide com o sentido atribuído
a
porque o sentido de percurso coincide com o sentido atribuído
a
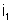 ; a f.e.m.
; a f.e.m.
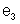 será tomada com o sinal - , porque o sentido de percurso
é o inverso do sentido atribuído
será tomada com o sinal - , porque o sentido de percurso
é o inverso do sentido atribuído
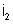 . O primeiro membro da equação será então,
. O primeiro membro da equação será então,
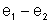
O
produto
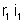 é positivo porque o sentido de percurso coincide com o sentido
de
é positivo porque o sentido de percurso coincide com o sentido
de
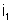 ; o produto
; o produto
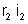 é negativo, porque o sentido de percurso não coincide com
o sentido de
é negativo, porque o sentido de percurso não coincide com
o sentido de
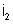 . O segundo membro da equação será então
. O segundo membro da equação será então
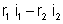 .
.
A
equação fica, portanto:
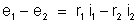
Podemos
aplicar novamente a segunda lei, agora à malha constituída pela pilha
(1) e pela resistência r.
Resulta:
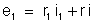
O
sistema de equações
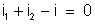 ,
,
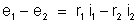 e
e
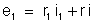 resolve o problema. Substituindo os valores numéricos, resulta:
resolve o problema. Substituindo os valores numéricos, resulta:

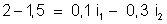 , ou
, ou
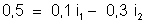
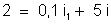
Resolvendo
esse sistema de equações encontraremos:
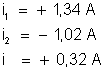
Os sinais positivos de i e
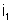 indicam que essas duas correntes tem realmente os sentidos
que no início tínhamos atribuído arbitrariamente. O sinal negativo
de
indicam que essas duas correntes tem realmente os sentidos
que no início tínhamos atribuído arbitrariamente. O sinal negativo
de
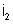 indica que o sentido dessa corrente é contrário naquele que
tínhamos atribuído. Portanto, os sentidos verdadeiros das correntes
são os que estão indicados na figura 183.
indica que o sentido dessa corrente é contrário naquele que
tínhamos atribuído. Portanto, os sentidos verdadeiros das correntes
são os que estão indicados na figura 183.
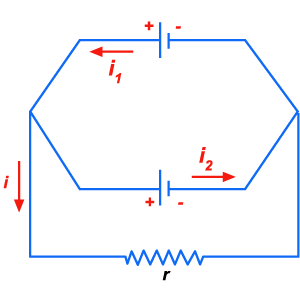
Figura 183
12. No
circuito ao lado as pilhas 1, 2 e 3 tem as seguintes características:
pilha
1: f.e.m.
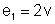 , resistência interna
, resistência interna

pilha
2: f.e.m.
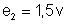 , resistência interna
, resistência interna
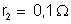
pilha
3: f.e.m.
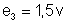 , resistência interna
, resistência interna
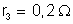 .
.
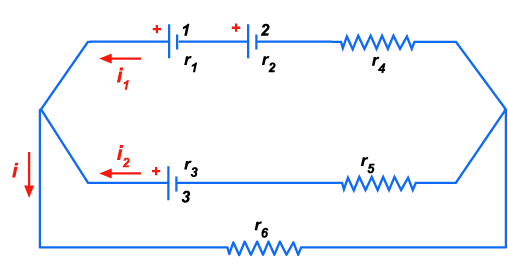
Figura 184
A
resistência
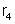 vale
vale
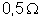 ,
,
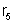 vale
vale
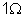 ,
,
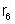 vale
vale
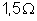 . Calcular: a) as intensidades das correntes
. Calcular: a) as intensidades das correntes
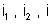 ; b) a potência dissipada na resistência
; b) a potência dissipada na resistência
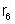 .
.
13. A
pilha do circuito do lado tem f.e.m. 1,5 v e resistência interna
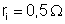 . As resistências
. As resistências
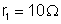 ;
;
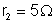 ;
;
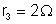 , e
, e
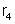 é desconhecida. Calcular o valor de
é desconhecida. Calcular o valor de
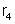 para que não passe corrente pelo galvanômetro. Resposta:
para que não passe corrente pelo galvanômetro. Resposta:
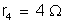 .
.
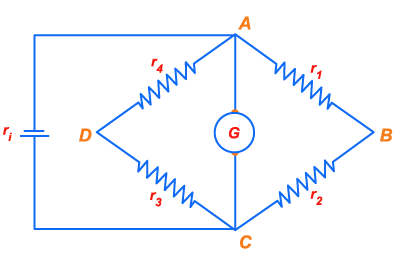
Figura 185
14. Defina
f.e.m. de um gerador, e justifique a definição.
15. Como
se calcula a potência fornecida por um gerador? E a energia?
16. Quando
a corrente elétrica é conduzida nos metais, as cargas elétricas caminham
do polo positivo do gerador para o negativo, ou do negativo para o
positivo?
17. Deduza
a lei de Poullet.
18. Examine
a fórmula
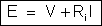 .
Por esse exame, acha que a resistência interna de um gerador deve
ser grande ou pequena? Porque?
.
Por esse exame, acha que a resistência interna de um gerador deve
ser grande ou pequena? Porque?
19. Deduza
as características de uma associação em série de geradores. E as
de uma associação em paralelo de geradores iguais.
20. Quando
em uma associação em paralelo os geradores são iguais, aplicamos as
fórmulas
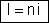 ,
,
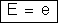 e
e
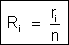 .
Mas, quando os geradores são diferentes, como se resolve o problema?
.
Mas, quando os geradores são diferentes, como se resolve o problema?
21. Defina
f.c.e.m. de um receptor, e justifique a definição.
22. Porque
as unidades de f.e.m. e f.c.e.m. são as mesmas unidades de diferença
de potencial?
23. Deduza
a expressão que dá a diferença de potencial entre dois pontos de um
circuito em função das f.e.m. e f.c.e.m. existentes entre esses dois
pontos. Qual a importância dessa expressão?
24. Deduza
as duas leis de Kirchhoff. E mostre como elas devem ser aplicadas
.
Autor:
Roberto A. Salmeron