
1. Calcular a
intensidade de uma corrente elétrica, suposta constante, sabendo que
por uma secção transversal do condutor passa a carga de 2 coulombs
durante 5 segundos. Resposta no sistema MKS e no CGSES.
Por definição,
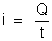
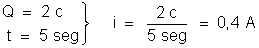
Para transformar
a resposta para o sistema CGSES podemos fazer a seguinte proporção:
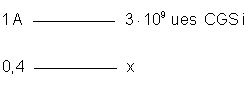
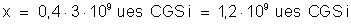
Resposta:
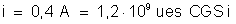 .
.
2. Qual a carga
elétrica que passa pela secção transversal de um condutor durante
uma hora, sabendo-se que a intensidade da corrente é constante e vale
2 ampères?
3. A
diferença de potencial entre dois pontos de um condutor é 10 volts.
A intensidade da corrente é constante e é igual a 4 ampères.
Qual a resistência e a condutância entre esses dois pontos do condutor?

Pela lei de Ohm,
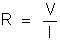
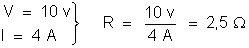

4. A diferença
de potencial entre dois pontos de um condutor é 16 v, e a resistência
é
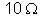 . a) Qual a intensidade da corrente que circula? b) Qual
a condutância do condutor?
. a) Qual a intensidade da corrente que circula? b) Qual
a condutância do condutor?
5. Calcular
a diferença de potencial entre dois pontos de um condutor, sabendo
que a intensidade da corrente é 5 A e que a resistência entre dois
pontos vale
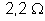 .
.
6. A resistência
de um condutor é
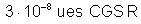 . Calcular a diferença de potencial entre os extremos do condutor
em volts, sabendo que a intensidade da corrente que circula é um miliampère.
. Calcular a diferença de potencial entre os extremos do condutor
em volts, sabendo que a intensidade da corrente que circula é um miliampère.
7. A diferença
do potencial entre os extremos de um condutor é
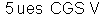 . A intensidade da corrente é constante de 100 mA. a) Calcular
a resistência em
. A intensidade da corrente é constante de 100 mA. a) Calcular
a resistência em
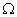 e em
e em
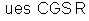 . b) Calcular a condutância.
. b) Calcular a condutância.
8. Um condutor
AB de resistência
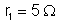 é ligado em série com um condutor BC de resistência
é ligado em série com um condutor BC de resistência
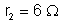 . A intensidade da corrente que passa por
. A intensidade da corrente que passa por
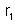 é de 2 A. Calcular: a) a intensidade da corrente que passa
por
é de 2 A. Calcular: a) a intensidade da corrente que passa
por
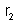 ; b) a diferença de potencial entre A e B, e entre B e C; c) a
resistência total; d) a diferença de potencial entre A e C.
; b) a diferença de potencial entre A e B, e entre B e C; c) a
resistência total; d) a diferença de potencial entre A e C.
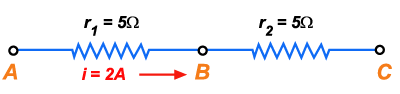
Figura 136
9. São associados
em série três condutores cujas resistências valem respectivamente
1, 2 e 3 ohms. A diferença de potencial entre os extremos da
associação é 60 volts. Calcular a diferença de potencial entre
os extremos de cada condutor.
10. São associados
em série três condutores cujas resistências valem 5, 12 e 15 ohms.
A diferença de potencial entre os extremos do primeiro é 12 volts.
Calcular: a) a intensidade da corrente elétrica que passa pela
associação; b) a diferença de potencial entre os extremos dos
condutores de 12 e 15 ohms, respectivamente; c) a diferença
de potencial entre os extremos da associação.
11. São associados
em paralelo dois condutores cujas resistências valem respectivamente
2 e 3 ohms. Pelo primeiro passa uma corrente elétrica de intensidade
constante de 5 ampères. Calcular: a) a diferença de potencial
entre os extremos de cada condutor; b) a intensidade da corrente
que passa pelo outro condutor; c) a intensidade da corrente
fora da associação; d) a resistência total da associação.

Figura 137

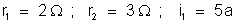
a) Aplicando
a lei de Ohm ao condutor de resistência
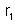 , temos :
, temos :
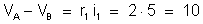
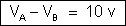
e essa diferença
de potencial é igual para os dois condutores.
b) Aplicando
a lei de Ohm ao condutor de resistência
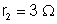 , temos:
, temos:
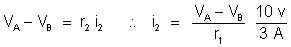
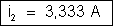
c) Por uma
das leis de Kirchhoff:
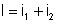
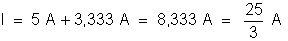
d) Pela outra
lei de Kirchhoff:
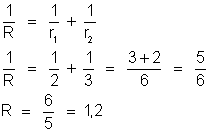
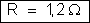
Prova – Podemos
conferir o problema aplicando a lei do Ohm ao condutor equivalente
à associação:
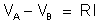
Devemos
encontrar o mesmo valor de 10 v já calculado. Temos:
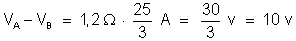
portanto,
confere.
12.
São associados em paralelo três condutores cujas resistências valem
respectivamente
 e
e
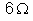 . A intensidade total da corrente é
. A intensidade total da corrente é
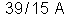 . Calcular: a) a resistência total da associação; b) a
diferença de potencial entre os extremos da associação; c) a
intensidade da corrente em cada derivação.
. Calcular: a) a resistência total da associação; b) a
diferença de potencial entre os extremos da associação; c) a
intensidade da corrente em cada derivação.
13.
Demonstrar que, quando duas resistências
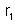 e
e
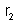 são associadas em paralelo, a resistência equivalente R é menor do
que
são associadas em paralelo, a resistência equivalente R é menor do
que
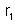 e menor do que
e menor do que
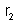 .
.
14.
Na figura a seguir são conhecidos:
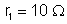 ,
,
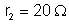 ,
,
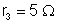 ,
,
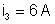 . Calcular: a) a resistência total entre A e C; b) a
corrente I; c) as correntes
. Calcular: a) a resistência total entre A e C; b) a
corrente I; c) as correntes
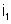 e
e
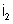 ; d) as dif'erenças de potencial entre A e B, entre B e C, entre
A e C.
; d) as dif'erenças de potencial entre A e B, entre B e C, entre
A e C.
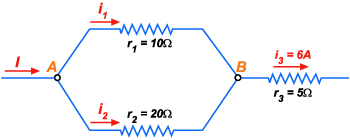
Figura 138
15.
Um resistor de resistência
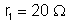 é associado em paralelo com outro resistor de resistência
é associado em paralelo com outro resistor de resistência
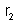 desconhecida. A intensidade da corrente fora da associação é 5A.
A diferença de potencial entre os extremos da associação é 12A. Calcular
desconhecida. A intensidade da corrente fora da associação é 5A.
A diferença de potencial entre os extremos da associação é 12A. Calcular
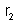 .
.
16.
Dado o circuito elétrico ao lado, calcular: a) a resistência
total entre A e D; b) as diferenças de potencial entre A e B,
entre B e C , entre C e D, entre A e D, sabendo que
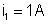 .
.
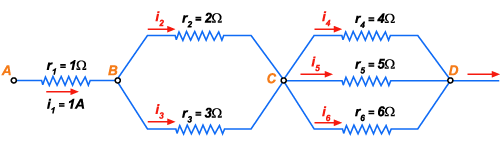
Figura 139
17.
Um condutor filiforme tem comprimento de 2 m, área de secção
transversal de
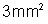 e resistividade de
e resistividade de
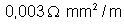 . Calcular a resistência:
. Calcular a resistência:

A
resistência do condutor, em função das dimensões, é dada por
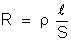
Temos
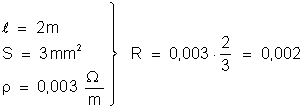
Resposta:
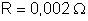 .
.
18. Um
condutor tem diâmetro de 1mm, comprimento de 5m e é construído de
uma substância cuja resistividade vale
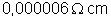 . Calcular a resistência.
. Calcular a resistência.
19.
Calcular a resistividade de uma substância sabendo que um fio construído
com essa substância, tendo 5 km de comprimento e 0,4 cm de diâmetro,
permite a passagem de uma corrente de 0,2 A, quando suporta a diferença
de potencial de 20 v.
20.
Na figura ao lado, o potencial do ponto B é igual ao potencial do
ponto D. A resistência
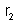 vale
vale
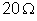 ;
;
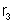 vale
vale
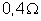 ;
;
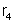 vale
vale
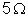 . Calcular
. Calcular
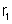 .
.
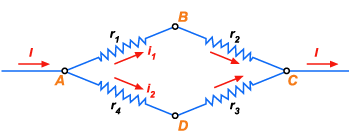
Figura 140
21.
No problema anterior, se o resistor de resistência
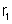 é cilíndrico e tem 1m de comprimento e 1mm de diâmetro, qual a sua
resistividade?
é cilíndrico e tem 1m de comprimento e 1mm de diâmetro, qual a sua
resistividade?
22.
Um condutor de resistência
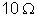 é percorrido por uma corrente de intensidade constante de 2 A. Calcular:
a) a potência absorvida pelo condutor; b) a energia absorvida
pelo condutor durante meia hora.
é percorrido por uma corrente de intensidade constante de 2 A. Calcular:
a) a potência absorvida pelo condutor; b) a energia absorvida
pelo condutor durante meia hora.

A
potência absorvida pelo condutor vale:
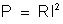 ou
ou
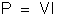
Temos:
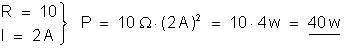
A
energia absorvida pelo condutor vale:
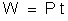
Temos:
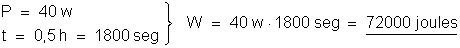
23.
São associadas em série três resistências: uma de
 , outra de
, outra de
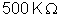 e outra desconhecida. A diferença de potencial entre os extremos
da associação é de 3000 v. Quanto deve valer a terceira resistência
para que a corrente seja de
e outra desconhecida. A diferença de potencial entre os extremos
da associação é de 3000 v. Quanto deve valer a terceira resistência
para que a corrente seja de
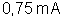 ?
?
24. Na
figura a seguir,
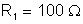 ,
,
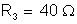 o potencial do ponto A é 225 v e o do ponto D é nulo. a) Qual
deve ser a resistência
o potencial do ponto A é 225 v e o do ponto D é nulo. a) Qual
deve ser a resistência
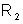 para que o potencial do ponto B seja 105 v? b) Qual a potência
dissipada pela associação? c) Qual a energia dissipada pela
associação em 5 minutos?
para que o potencial do ponto B seja 105 v? b) Qual a potência
dissipada pela associação? c) Qual a energia dissipada pela
associação em 5 minutos?

Figura 141
25.
Certo “ferro de passar roupa” tem resistência de
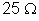 , e a corrente máxima que pode passar por essa resistência
é de 5 A. Dispõe-se de uma diferença de potencial de 220 v, à qual
o “ferro” deve ser ligado. Mas, se ele for ligado diretamente a essa
diferença de potencial, a corrente será maior que 5 A, e a resistência
do “ferro” se queimará. Liga-se, então, em série com a resistência
do “ferro” uma outra resistência, para que a corrente não fique maior
que 5 A. Pergunta-se: a) qual seria a corrente se a resistência
do “ferro” fosse ligada sozinha aos 220 v? b) Qual deve ser
o valor mínimo da resistência ligada em série? c) Qual a potência
máxima que esse “ferro” pode consumir?
, e a corrente máxima que pode passar por essa resistência
é de 5 A. Dispõe-se de uma diferença de potencial de 220 v, à qual
o “ferro” deve ser ligado. Mas, se ele for ligado diretamente a essa
diferença de potencial, a corrente será maior que 5 A, e a resistência
do “ferro” se queimará. Liga-se, então, em série com a resistência
do “ferro” uma outra resistência, para que a corrente não fique maior
que 5 A. Pergunta-se: a) qual seria a corrente se a resistência
do “ferro” fosse ligada sozinha aos 220 v? b) Qual deve ser
o valor mínimo da resistência ligada em série? c) Qual a potência
máxima que esse “ferro” pode consumir?
26.
São ligadas em paralelo duas resistências, uma de
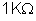 e outra desconhecida; entre dois pontos cuja diferença de potencial
é de 200 v. a) Quanto deve valer a resistência desconhecida
para que a potência dissipada pela associação seja de 240 w? b) Qual
a corrente que passa por cada uma das resistências? c) Qual
a condutância da associação?
e outra desconhecida; entre dois pontos cuja diferença de potencial
é de 200 v. a) Quanto deve valer a resistência desconhecida
para que a potência dissipada pela associação seja de 240 w? b) Qual
a corrente que passa por cada uma das resistências? c) Qual
a condutância da associação?
27.Certo
reostato tem resistência variável de 0 a
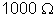 . A corrente máxima que ele pode suportar é de 0,4. a) Qual
a máxima diferença de potencial a que ele pode ser ligado? b) Qual
a potência máxima que ele pode dissipar?
. A corrente máxima que ele pode suportar é de 0,4. a) Qual
a máxima diferença de potencial a que ele pode ser ligado? b) Qual
a potência máxima que ele pode dissipar?
28. Dispõe-se
de um gerador de 200 v para fornecer corrente a uma resistência
AB de
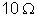 . Como o fabricante
dessa resistência indicou que a potência máxima que ela pode
dissipar é 1 quilowatt, ela não pode ser ligada diretamente
aos 200 v, porque consumiria mais que 1 quilowatt. Então
se liga em série com ela o reostato de variação descontínua,
como indica a figura ao lado, para diminuir a intensidade
da corrente. Pergunta-se: a) que potência seria consumida
pelos . Como o fabricante
dessa resistência indicou que a potência máxima que ela pode
dissipar é 1 quilowatt, ela não pode ser ligada diretamente
aos 200 v, porque consumiria mais que 1 quilowatt. Então
se liga em série com ela o reostato de variação descontínua,
como indica a figura ao lado, para diminuir a intensidade
da corrente. Pergunta-se: a) que potência seria consumida
pelos
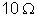 se fosse ligada
diretamente aos 200 v? b) quando ligado o reostato, a
haste a deve ser ligada em qual dos pontos B, C, D e E? se fosse ligada
diretamente aos 200 v? b) quando ligado o reostato, a
haste a deve ser ligada em qual dos pontos B, C, D e E? |
 Figura 142 Figura 142 |
29.
Na figura a seguir, o potencial do ponto A é 200 v, e o do ponto B
de 40 v. As resistências de 20, 60 e
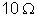 estão em série
com um reostato cuja resistência pode variar de 0 a
estão em série
com um reostato cuja resistência pode variar de 0 a
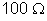 . a) Para que a diferença de potencial suportada pela resistência
de
. a) Para que a diferença de potencial suportada pela resistência
de
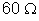 seja máxima, o cursor C do reostato deve ficar em M ou em D? b) Qual
é essa diferença de potencial máxima? c) Para que essa diferença
de potencial seja mínima, onde deve ficar o cursor? d) Qual
é essa diferença de potencial mínima?
seja máxima, o cursor C do reostato deve ficar em M ou em D? b) Qual
é essa diferença de potencial máxima? c) Para que essa diferença
de potencial seja mínima, onde deve ficar o cursor? d) Qual
é essa diferença de potencial mínima?
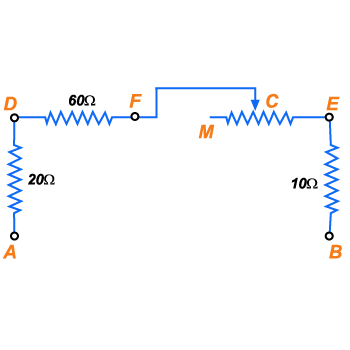
Figura 143
30. Mesmo
enunciado do problema anterior, para o caso em que a resistência de
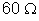 está em paralelo com o reostato MD, como indica a figura. Compare
os resultados dos problemas 29 e 30.
está em paralelo com o reostato MD, como indica a figura. Compare
os resultados dos problemas 29 e 30.
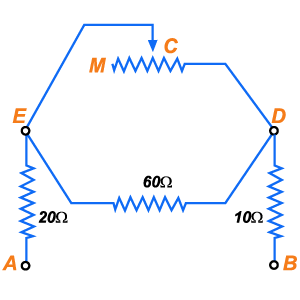
Figura 144
31.
A resistividade do cobre a 0oC é
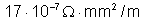 , e o coeficiente de temperatura 0,004
, e o coeficiente de temperatura 0,004
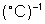 . Um condutor de cobre tem diâmetro de 0,5 mm e comprimento
de 50 m. a) Qual é a resistência e a condutância do condutor
a 0oC? b) Qual a resistência e a condutância a 100oC?
c) De quantos por cento aumentou a resistêcia, quando a temperatura
passou de 0oC a 100oC? d) Ligado entre
dois pontos cuja diferença de potencial é 0,1 v, qual a potência absorvida
pelo condutor quando ele está a 0oC? e) E quando
ele está a 100oC?
. Um condutor de cobre tem diâmetro de 0,5 mm e comprimento
de 50 m. a) Qual é a resistência e a condutância do condutor
a 0oC? b) Qual a resistência e a condutância a 100oC?
c) De quantos por cento aumentou a resistêcia, quando a temperatura
passou de 0oC a 100oC? d) Ligado entre
dois pontos cuja diferença de potencial é 0,1 v, qual a potência absorvida
pelo condutor quando ele está a 0oC? e) E quando
ele está a 100oC?
Nota: Ao
resolver os exercícios 32, 33, 34 e 35 não se esqueça de que as resistividades
dadas na Tabela valem para 0oC.
32.
Um fio de prata tem secção transversal de
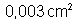 e comprimento de 2000 cm. a) Qual a sua resistência
e sua condutância a 0oC? b) E a 50oC?
(Tire da Tabela
os dados que quiser).
e comprimento de 2000 cm. a) Qual a sua resistência
e sua condutância a 0oC? b) E a 50oC?
(Tire da Tabela
os dados que quiser).
33.
Uma resistência padrão feita de niquelina tem um valor padrão R a
0oC. Se ela for usada a 30oC, por que número
deve ser multiplicado o valor marcado R para que se tenha o valor
verdadeiro a 30oC? (Tire da Tabela I os dados que
quiser).
34. Um
fio de níquel tem resistência de
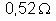 a 80oC. a) Qual a sua resistência a 20oC?
b) Qual sua secção transversal, sabendo que seu comprimento é
1000 cm? (Tire da Tabela
os dados que quiser)
a 80oC. a) Qual a sua resistência a 20oC?
b) Qual sua secção transversal, sabendo que seu comprimento é
1000 cm? (Tire da Tabela
os dados que quiser)
35.
Dispõe-se de um fio de níquel de área de secção transversal
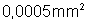 . Quer-se construir com ele um reostato que tenha
. Quer-se construir com ele um reostato que tenha
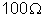 a 50oC. a) Quantos metros de fio devem ser
usados? (Tire da Tabela os
dados que
quiser). b) Acha o leitor que seria cômodo usar esse fio para
a construção do reostato?
a 50oC. a) Quantos metros de fio devem ser
usados? (Tire da Tabela os
dados que
quiser). b) Acha o leitor que seria cômodo usar esse fio para
a construção do reostato?
36. As
resistências que constituem certa caixa de resistências tem os seguintes
valores:
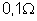 ,
,
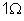 ,
,
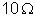 ,
,
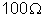 ,
,
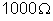 . Faça uma lista de todos os valores de resistência que se
podem obter com essa caixa.
. Faça uma lista de todos os valores de resistência que se
podem obter com essa caixa.
37. Em
uma solução de cloreto de sódio em água são mergulhadas duas
placas metálicas idênticas A e B, de área
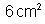 , paralelas e afastadas de 10cm. Aplicando-se uma diferença
de potencialde 200 v entre as placas, um amperômetro em série
com elas registra uma corrente de 0,2 A. Qual a resistividade
e a condutividade da solução?
, paralelas e afastadas de 10cm. Aplicando-se uma diferença
de potencialde 200 v entre as placas, um amperômetro em série
com elas registra uma corrente de 0,2 A. Qual a resistividade
e a condutividade da solução?

As soluções
de ácidos, bases e sais em água são condutores que obedecem
as mesmas leis que os condutores metálicos. As duas placas
determinam na solução um prisma de base
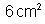 e altura de 100 cm. A
esse condutor prismático podemos aplicar a equação:
e altura de 100 cm. A
esse condutor prismático podemos aplicar a equação:
|
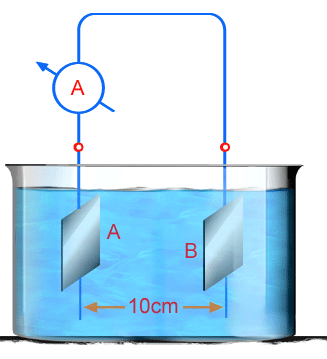 Figura 145 Figura 145 |
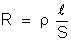
Temos:
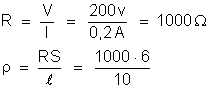
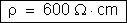
A
condutividade é:
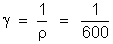
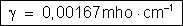
38.
Na cuba da figura 146 há uma solução de ácido sulfúrico em água,
de resistividade
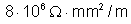 . São imersas na solução duas placas metálicas paralelas, idênticas,
de
. São imersas na solução duas placas metálicas paralelas, idênticas,
de
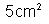 cada e afastadas de 8 cm. A essas placas metálicas são ligadas as
resistências de 200, 300 e
cada e afastadas de 8 cm. A essas placas metálicas são ligadas as
resistências de 200, 300 e
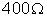 , conforme indica a figura. Aplicando-se certa diferença de potencial
V entre os extremos A e B do conjunto, pela resistência de
, conforme indica a figura. Aplicando-se certa diferença de potencial
V entre os extremos A e B do conjunto, pela resistência de
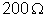 passa uma corrente de
passa uma corrente de
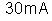 . a) Qual valor de V? b) Qual a potência dissipada pela
solução? c) Qual a energia dissipada pela solução em uma hora?
. a) Qual valor de V? b) Qual a potência dissipada pela
solução? c) Qual a energia dissipada pela solução em uma hora?
39.
O que é um íon? Dê dez exemplos.
40. O
que é a corrente elétrica?
41. Quais
os principais efeitos da corrente elétrica?
42. Quais
os diferentes tipos de condução elétrica? Do que consiste a corrente
elétrica nos metais? A condução de eletricidade nos gases é mais
parecida com a condução nos metais ou nas soluções? Por que?
43. Defina
intensidade de corrente elétrica.
44. Deduza
a relação entre um microampère e a
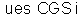 . E entre um miliampère e a
. E entre um miliampère e a
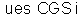 .
.
45. Enuncie
a lei de Ohm. Defina resistência elétrica de um condutor.
46.
Defina resistividade de um material.
47. Defina
a
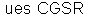 e o ohm absoluto.
e o ohm absoluto.
48. Defina
ohm internacional e ampère internacional.
49. Quais
as unidades fundamentais do sistema MKS? E quais as do sistema CGSES?
50. Deduza
a relação entre a unidade de condutância do sistema do CGSES e a do
MKS. Idem com as unidades de condutividade. 13 – Deduza
a relação entre o miliohm e a
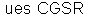 . E entre o microhm e a
. E entre o microhm e a
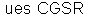 .
.
51. Como
varia a resistividade em função da temperatura?
52. No
tópico "Variação
da Resistência com a Temperatura" foi colocado um quadro
com valores de resistividade e coeficiente de temperatura de diversos
materiais. Qual dos materiais dados nesse quadro é melhor condutor?
Qual o pior? Por que?
53. Qual
das substâncias da Tabela
o leitor usaria para construir um padrão de resistência? Por que?
54.
Demonstre que o coeficiente de temperatura é o inverso de uma temperatura.
55.
O que é supercondutividade? E supercondutor?
56.
Defina as seguintes unidades do sistema MKB: ampère, volt, coulomb.
57.
Existe uma unidade de resistividade chamada
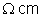 . Como se define essa unidade?
. Como se define essa unidade?
58.
Quais as diferenças entre uma caixa de resistência e um reostato?
59. Demonstre
as características de uma associação em série de resistências.
60. Demonstre
as características de uma associação em paralelo de resistências.
61. Deduza
a fórmula que exprime a energia absorvida por um condutor.
62. Recapitule
as definições das unidades do sistema CGSES, partindo das suas unidades
fundamentais.
63.
Idem para o MKB.