
Já
introduzimos o conceito de constante dielétrica quando deduzimos
a fórmula de Coulomb. Seja
 a constante dielétrica de um isolante qualquer, e
a constante dielétrica de um isolante qualquer, e
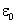 a do vácuo. Chama-se constante dielétrica relativa, ou
poder indutor específico relativo de um isolante ao quociente da
sua constante dielétrica pela constante dielétrica do vácuo. Representaremos
por K. Então:
a do vácuo. Chama-se constante dielétrica relativa, ou
poder indutor específico relativo de um isolante ao quociente da
sua constante dielétrica pela constante dielétrica do vácuo. Representaremos
por K. Então:
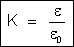
É um número, não tem unidades, pois é o quociente de duas grandezas
da mesma espécie.
Imaginemos
um condensador qualquer cujo dielétrico tenha constante dielétrica
 , por exemplo, um condensador plano. Sua capacidade é:
, por exemplo, um condensador plano. Sua capacidade é:
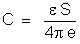 , donde
tiramos
, donde
tiramos
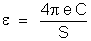 .
.
O
mesmo condensador, tendo vácuo como isolante, terá a capacidade:
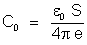 , donde tiramos
, donde tiramos
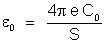 .
.
Vemos
então que
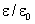 é igua1 a
é igua1 a
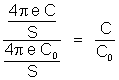
Logo,
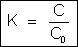
Concluímos
que também podemos definir a constante dielétrica relativa de um
isolante do seguinte modo: é o quociente da capacidade de um condensador
qualquer feito com esse isolante pela capacidade do mesmo condensador
tendo o vácuo como dielétrico.
Nota: No
sistema CGSES a constante dielétrica do vácuo,
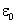 , é igual a um. Então, nesse sistema,
, é igual a um. Então, nesse sistema,
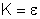 , numericamente. Isso é uma desvantagem, porque K é um simples
número, ao passo que
, numericamente. Isso é uma desvantagem, porque K é um simples
número, ao passo que
 é uma grandeza e, portanto, tem unidades.
é uma grandeza e, portanto, tem unidades.

Neste
livro estamos chamando constante dielétrica, ou poder indutor específico
à constante
 , que aparece desde a fórmula de Coulomb, e constante dielétrica
relativa, ou poder indutor específico relativo à constante K. Mas,
muitos autores adotam outra nomenclatura: chamam permissividade
à constante
, que aparece desde a fórmula de Coulomb, e constante dielétrica
relativa, ou poder indutor específico relativo à constante K. Mas,
muitos autores adotam outra nomenclatura: chamam permissividade
à constante
 , e constante dielétrica ou poder indutor específico à constante
K. É preciso atenção a essa nomenclatura quando se lê um livro
de Eletricidade.
, e constante dielétrica ou poder indutor específico à constante
K. É preciso atenção a essa nomenclatura quando se lê um livro
de Eletricidade.