
| 1.
Uma carga elétrica puntiforme de 500 ues CGSq é
colocada no vácuo. Calcular o campo elétrico
que ela produz em um ponto A situado a de 10 cm distância. |
 Figura 75 Figura 75 |
a) módulo
do campo
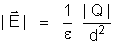


b) direção
de campo – a da retaQA
c) sentido do
campo – o do sentido QA.
| 2.
Uma carga elétrica puntiforme de -4 c está no
vácuo. Calcular o campo elétrico e o potencial
que ela produz em um ponto situado a 0,5 m de distância.
Resolver no sistema MKS. |
 Figura 76 Figura 76 |

1o) Cálculo
de campo elétrico.
a) Módulo:
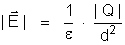
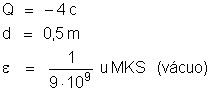
Resulta:
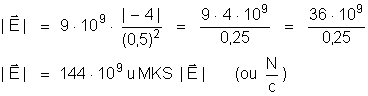
b) direção
– a da reta QA
c) sentido
– o do sentido QA.
2o) Cálculo
do potencial.
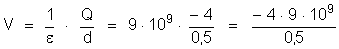
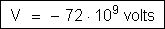
3. Duas
cargas elétricas puntiformes, valendo -400 ues CGSq
e 2.10-6 c, ocupam dois
vértices de um triângulo equilátero
de lado 0,20 m, no vácuo. Calcular o campo e o potencial
no outro vértice do triângulo. Resolver no
sistema CGSES e transformar os resultados para o MKS.

1o)
Cálculo do campo
|
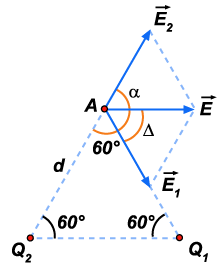 Figura 77 Figura 77 |
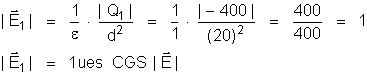
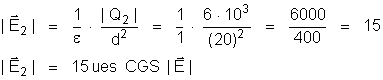
O módulo
do resultante será:
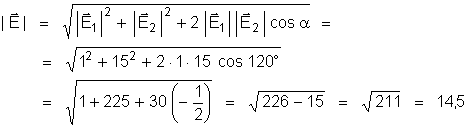
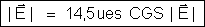
A
direção do campo resultante pode ser assinalada
pelo ângulo
 que ele faz com a componente
que ele faz com a componente
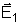 .
.
Temos:
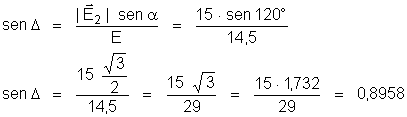
2o
) Cálculo do potencial.
O potencial
do ponto A é a soma algébrica dos potenciais que
Q1 e Q2
produzem separadamente em A, isto é:
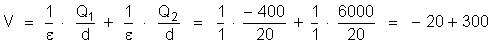

3o)
Mudança das unidades para o sistema MKS
a) Campo –
Podemos estabelecer a proporção:
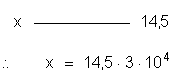
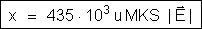
b) Potencial
– Podemos estabelecer a proporção
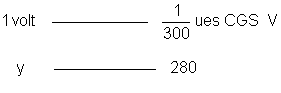

| 4.
Seis cargas elétricas puntitormes, todas positivas,
são colocadas no vácuo nos vértices de
um hexágono regular de lado 10 cm. As cargas valem,
respectivamente, em ues CGSq 100, 200, 300, 400, 500, 600.
Calcular o campo elétrico e o potencial que elas produzem
no centro do hexágono. |
 Figura 78 Figura 78 |
5. Uma esfera
de raio 15 cm é colocada no vácuo e carregada com
a carga elétrica de 200 ues CGSq. Calcular o campo elétrico
e o potencial: a) em um ponto da superfície da esfera; b)
em um ponto externo, situado a 5 cm da superfície; c) em
um ponto interno qualquer.
6. Uma esfera
colocada no vácuo tem raio de 10 cm e carga elétrica
de 200 ues CGSq. Calcular o campo elétrico e o potencial:
a) em um ponto de superfície da esfera; b) em um ponto externo
situado a 100 cm da superfície da esfera; c) em um ponto
interno qualquer. Calcular a força que atua sobre uma carga
q = 200 ues CGSq colocada; d) no ponto externo situado a 100 cm
da superfície; e) em um ponto interno qualquer.
7. Demonstrar,
com auxílio do teorema de Coulomb, que o campo elétrico
na superfície de uma esfera pode ser calculado imaginando-se
que a carga esteja concentrada no centro.
8. Calcular
o campo elétrico e o potencial na superfície de uma
esfera de raio 5 cm, sabendo que a carga elétrica da esfera
é -4.10-5 c (esfera colocada
no vácuo) .
9. Calcular
o campo elétrico em um ponto de uma superfície plana
retangular de dimensões 20cm x 40cm, carregada com carga
de 600 ues CGSq. Admitir a superfície no vácuo.
10. O campo
elétrico em um ponto de uma superfície plana é
5 ues CGSq
 .
Calcular a área da superfície, sabendo que a carga
é de 2.10-8 c . Admitir
a superfície no vácuo.
.
Calcular a área da superfície, sabendo que a carga
é de 2.10-8 c . Admitir
a superfície no vácuo.
11. O campo
elétrico em um ponto de uma superfície esférica
é 5 ues CGSq
 .
Calcular o raio da esfera, sabendo que a carga é de 20 statcoulombs.
Admitir a esfera no vácuo, e resolver o problema usando obrigatoriamente
o teorema de Coulomb.
.
Calcular o raio da esfera, sabendo que a carga é de 20 statcoulombs.
Admitir a esfera no vácuo, e resolver o problema usando obrigatoriamente
o teorema de Coulomb.
| 12.
No interior de um cubo é colocada uma carga elétrica
puntiforme de 40 statcoulombs. Calcular o fluxo total que
atravessa toda a superfície do cubo. O cubo está
no vácuo.

A
superfície do cubo sendo uma superfície fechada,
o fluxo através dessa superfície pode ser calculado
pelo teorema de Gauss
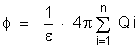 |
 Figura 79 Figura 79 |
Há só
uma carga no interior do tubo. Então:
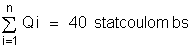
Resulta:
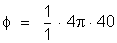
Resposta:
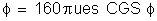 .
.
13. No interior
de uma superfície fechada qualquer, são colocadas
as cargas elétricas seguintes:
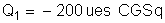 ,
,
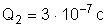 ,
,
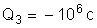 .
Calcular o fluxo total através da superfície. Dar
a resposta no sistema CGSES e no MKS.
.
Calcular o fluxo total através da superfície. Dar
a resposta no sistema CGSES e no MKS.
14. Calcular
o fluxo que atravessa uma superfície plana de 50 cm2,
colocada perpendicularmente a um campo elétrico uniforme
de intensidade 3 ues CGSq
 .
.
15. Calcular
o fluxo que atravessa uma superfície plana de 80 cm2
área colocada de maneira a fazer ângulo de 30o
com a direção de um campo elétrico
uniforme de intensidade 6 ues CGSq
 .
.
16. Calcular
o fluxo que atravessa uma superfície plana de 100 cm2
área colocada em um campo elétrico uniforme de intensidade
15 ues CGSq
 nos seguintes casos:
nos seguintes casos:
a) a normal
à superfície faz ângulo de 0o
com o campo;
b) a normal à superfície faz ângulo de 90o
com o campo;
c) a normal à superfície faz ângulo de 180o
com o campo;
d) a normal à superfície faz ângulo de 270o
com o campo;
e) a normal à superfície faz ângulo de 360o
com o campo.
Dar as respostas
em unidades CGSES e MKS.
17. Um campo
elétrico é produzido por uma carga elétrica
puntiforme de 100 statcoulombs, no vácuo. Calcular: a) potencial
de um ponto situado à distância de 0,50 m dessa carga;
b) a energia potencial de uma carga de 25 statcoulombs colocada
nesse ponto.
18. Um campo
elétrico é produzido no vácuo por duas cargas
elétricas puntiformes de 2 c e -5 c, respectivamente. Calcular:
a) o potencial de um ponto que dista 20 cm da primeira carga e 0,50
m da segunda; b) a energia potencial de uma carga elétrica
puntiforme de 0,06 c colocada nesse ponto. Resolver o problema no
sistema MKS.
19. Uma carga
elétrica puntiforme de 2 c é deslocada em um campo
elétrico, de um ponto de potencial 5 volts para um ponto
de potencial 2 volts. Qual o trabalho realizado pela força
eletrostática?

Quando uma
carga elétrica , abandonada em um campo elétrico,
é deslocada de um ponto de potencial para um ponto de potencial
, o trabalho realizado pelo campo é:
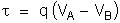
Temos
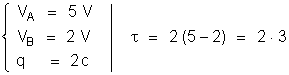
Resposta:
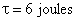 .
.
20. Uma carga
elétrica puntiforme de 10 c passou de um ponto de potencial
8 v a um ponto de potencial 5 v. Essa carga ganhou ou perdeu energia?
Quanto?
21. Uma carga
elétrica puntiforme de 8 ues CGSq é deslocada de um
ponto de potencial 3 ues CGSq a um ponto de potencial 2100 v. Essa
carga ganhou ou perdeu energia? Quanto? O trabalho foi realizado
pelo campo elétrico, ou contra o campo elétrico?
22. Uma carga
elétrica puntiforme de 5 c é deslocada de um ponto
de potencial 120 volts ao infinito. Calcular: a) o trabalho realizado;
b) a energia potencial da carga colocada no ponto de potencial 120
volts.
23.Qual a variação
da energia potencial de uma carga elétrica puntiforme de
3 c quando passa de um ponto de potencial 2 statvolts a um ponto
de potencial 4 statvolts?
24. Uma carga
elétrica puntiforme de 5 c abandonada em um campo elétrico
é deslocada de um ponto de potencial 50 v a um ponto de potencial
V desconhecido. Nesse deslocamento a carga absorve a energia de
20 joules. Calcular V.
25. Estabelecer
a relação existente entre a unidade de intensidade
de campo do sistema CGSES e a do sistema Giorgi, mas, usando obrigatoriamente
a expressão:
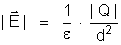
26. Se uma
carga negativa passa de certo potencial para outro mais alto, ela
ganha ou perde energia? E se for positiva?
27. Em Física
Atômica se usa uma unidade de energia chamada elétron-volt.
Um elétron-volt é o trabalho realizado para deslocar
a carga elétrica de um elétron entre dois pontos cuja
diferença de potencial é um volt. Sabendo que a carga
elétrica de um elétron é de 4,8021.10-10
ues CGSq, calcular a relação entre o erg e o elétron-volt.
28. Uma esfera
de raio tem densidade elétrica de 200 ues CGSq/cm2,
e está colocada num meio cuja constante dielétrica
é 8/9.108 u MKS. Calcular:
a) o campo elétrico e o potencial na superfície da
esfera; b) o campo elétrico e o potencial num ponto situado
a 5 cm da superfície da esfera; c) o fluxo elétrico
que atravessa a superfície de uma esfera de 20 cm de raio
concêntrica com a esfera eletrizada; d) o trabalho realizado
ao deslocar uma carga de 2.10-8
c da superfície da esfera eletrizada ao fim do seu campo.
29. O que é
um campo de forças? O que é campo elétrico
de uma carga elétrica?
30. Porque
o campo elétrico é newtoniano?
31. Defina vetor
campo elétrico em um ponto. Qual o módulo, a direção
e o sentido do vetor campo em um determinado ponto?
32. Defina a
unidade de intensidade de campo elétrico do sistema CGSES,
a do MKS, e mostre a relação entre elas.
33. Defina linha
de força de um campo eletrostático. Qual a importância
do conhecimento das linhas de força? Como se estabelece o
sentido de uma linha de força?
34. Desenhe
as linhas de força do campo produzido por duas cargas elétricas
de mesmo sinal. E do campo produzido por três cargas elétricas
de mesmo sinal dispostas nos vértices de um triângulo
equilátero (indique os sentidos das linhas).
35. Por que
duas linhas de força de um mesmo campo não se cruzam?
36. Defina campo
eletrostático uniforme. Dê exemplo.
37. Defina fluxo
eletrostático. Faça um gráfico da variação
do fluxo em função do ângulo que a normal à
superfície faz com o campo.
38. Defina as
unidades de fluxo dos sistemas CGSES e MKS, e mostre a relação
entre elas.
39. Defina tubo
de força. Qual é a forma geométrica de um tubo
de forças do campo produzido por uma carga elétrica
puntiforme?
40. Enuncie
e demonstre o teorema de Gauss.
41. Demonstre
que o campo eletrostático é nulo no interior de uma
esfera.
42. Demonstre
a fórmula que exprime o módulo do campo nas vizinhanças
de um plano.
43. Enuncie
e demonstre o teorema de Coulomb.
44. Defina tensão
eletrostática. Demonstre a fórmula (18).
45. Demonstre
que, no campo criado por um condutor esférico tudo se passa
como se a carga estivesse concentrada no centro da esfera.
46. Defina potencial
de um ponto de um campo eletrostático. Por que se chama potencial?
Se o potencial de um ponto é , qual a energia potencial de
uma carga colocada nesse ponto?
47. Demonstre
a fórmula (37).
48. Quanto vale
o potencial de um ponto da superfície de uma esfera eletrizada?
49. Quais as
unidades de diferença de potencial dos sistemas CGSES e MKS?
Qual a relação entre elas?
50. O que é
uma superfície equipotencial? Que direção tem
as linhas de força na superfície de um condutor eletrizado?
Por que?
51. O que é
blindagem eletrostática?
52. Descreva
a analogia existente entre o campo elétrico e o campo gravitacional.
53. Uma determinada
carga elétrica produz campo elétrico mais forte no
ar ou na água? Por que?
54. O fluxo
elétrico é uma grandeza escalar ou vetorial? Por que?