
Nota:
Antes de vermos a definição de fluxo elétrico,
vejamos um problema de Mecânica.
Imaginemos
que num canal de secção transversal constante
esteja escoando água com velocidade constante
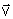 .
Consideremos uma secção qualquer plana de área
S no canal. Calculemos o volume de água que passa por
essa secção durante um segundo. Uma gota d’água
que num instante qualquer está em S, depois de um segundo
terá percorrido uma distância igual ao módulo
da velocidade, .
Consideremos uma secção qualquer plana de área
S no canal. Calculemos o volume de água que passa por
essa secção durante um segundo. Uma gota d’água
que num instante qualquer está em S, depois de um segundo
terá percorrido uma distância igual ao módulo
da velocidade,
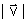 .
Então, o volume de água que passa por S em um
segundo é o volume de um cilindro gerado por S se S
deslocar-se paralelamente a sí mesmo de uma distância
igual a .
Então, o volume de água que passa por S em um
segundo é o volume de um cilindro gerado por S se S
deslocar-se paralelamente a sí mesmo de uma distância
igual a
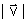 . . |
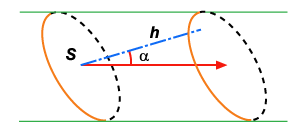
Figura 56-a |
O volume desse
cilindro é igual ao produto da área da base, S, pela
altura h (perpendicular comum às bases)(fig. 56-a). Representaremos
esse volume por
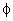 :
:
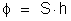
Sendo o ângulo
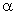 que faz com
que faz com
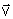 ,
vemos pela figura que:
,
vemos pela figura que:
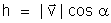
Substituindo
em
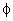 ,
teremos :
,
teremos :
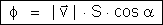
Concluímos
que o volume de água que atravessa a superfície de
área num segundo é dado pelo produto do módulo
da velocidade, pela área da superfície, pelo coseno
do ângulo que a normal à superfície faz com
a velocidade.

Figura 56
Esse volume
é chamado vazão, ou fluxo de água que atravessa
a superfície S.
Insistamos
então no seguinte: o fluxo
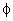 de água é dado pelo produto de três fatores:
o módulo de uma grandeza vetorial (velocidade), uma área
e um coseno. Essa expressão
de água é dado pelo produto de três fatores:
o módulo de uma grandeza vetorial (velocidade), uma área
e um coseno. Essa expressão
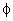 dada pela fórmula anterior é muito importante. Ela
é importante sob o aspecto matemático porque se conhecermos
certas propriedades da grandeza
dada pela fórmula anterior é muito importante. Ela
é importante sob o aspecto matemático porque se conhecermos
certas propriedades da grandeza
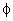 poderemos depois concluir propriedades da grandeza
poderemos depois concluir propriedades da grandeza
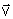 ,
e, como consequência, propriedades do movimento daquele líquido
no canal.
,
e, como consequência, propriedades do movimento daquele líquido
no canal.

Suponhamos uma
superfície plana de área colocada num campo elétrico
uniforme de intensidade
 .
Seja n a normal à superfície e
.
Seja n a normal à superfície e
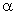 o ângulo que a normal faz com as linhas de força do
campo (fig. 57).
o ângulo que a normal faz com as linhas de força do
campo (fig. 57).
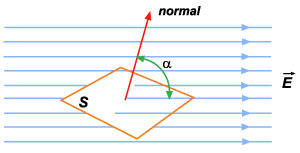
Figura 57
Por definição,
chama-se fluxo elétrico que atravessa uma superfície
plana colocada num campo elétrico uniforme ao produto da
área da superfície, pelo módulo do campo, pelo
coseno do ângulo que a normal à superfície faz
com a direção do campo. Representaremos por
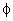 :
:
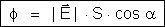
Vemos então
que o fluxo elétrico é definido-por analogia com o
fluxo de água. Acontece, porém, que o fluxo de água
tem um significado físico fácil de se compreender:
representa um volume de água que passa por uma superfície
em um segundo. Enquanto que, do fluxo elétrico, não
podemos fazer uma imagem física: ele é simplesmente
uma expressão matemática na qual aparece o vetor
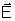 .
Veremos exemplos da importância dessa grandeza nos tópicos
"Teorema
de Coulomb" e "Campo
Elétrico Criado por Condutor Esférico",
nos quais, aplicando propriedades de
.
Veremos exemplos da importância dessa grandeza nos tópicos
"Teorema
de Coulomb" e "Campo
Elétrico Criado por Condutor Esférico",
nos quais, aplicando propriedades de
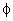 concluiremos propriedades do campo
concluiremos propriedades do campo
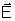 .
.
Quisemos colocar
antes o exemplo do fluxo de água para que o leitor perceba
bem que, embora o fluxo elétrico seja uma simples expressão
matemática que muito nos auxilia, a sua definição
foi copiada de uma fórmula que já existia, e que por
sua vez surgiu com um problema físico muito simples (o problema
de saber quanta água passa por uma secção de
um canal). O leitor deve ficar sempre prevenido com as definições.
Embora elas, em geral, sejam apresentadas sem maiores explicações,
é preciso lembrar que qualquer definição tem
sua origem física: não é um produto da imaginação.

Em muitas questões
interessa-nos saber se o fluxo que atravessa uma superfície
varia ou não, e, no caso de variar, como varia. Pela própria
definição de fluxo vemos que ele pode variar
de três modos:
1o
– variando o módulo campo
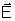 ;
;
2o – variando a área da superfície
S;
3o – variando o ângulo
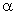 ,
isto é, a posição da superfície em
relação ao campo.
,
isto é, a posição da superfície em
relação ao campo.
Na prática
se usa o terceiro processo, por ser mais simples: faz-se a superfície
girar em torno de um eixo perpendicular ao campo para que haja variação
da posição da superfície em relação
ao campo.

Façamos
a superfície dar uma volta completa em torno de um eixo perpendicular
ao campo, partindo da posição em que
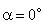 .
Permanecendo constantes os valores de
.
Permanecendo constantes os valores de
 e S, os valores do fluxo serão proporcionais aos de cos
e S, os valores do fluxo serão proporcionais aos de cos
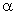 .
Durante essa variação do fluxo, poderemos considerar
alguns casos particulares que nos interessam, e que estão
assinalados nas figuras 58.
.
Durante essa variação do fluxo, poderemos considerar
alguns casos particulares que nos interessam, e que estão
assinalados nas figuras 58.
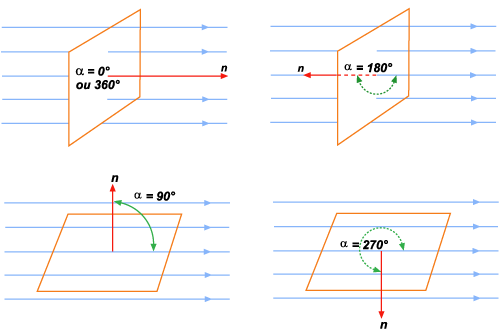
Figura 58
1o)
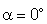 .
A superfície é perpendicular ao campo. Neste caso,
.
A superfície é perpendicular ao campo. Neste caso,
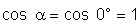 .
Fica:
.
Fica:
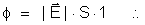
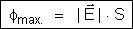
Como o valor
+1 é o máximo do coseno, neste caso temos o máximo
do fluxo.
2o)
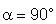 .
A superfície é paralela ao campo. Neste caso, cos
.
A superfície é paralela ao campo. Neste caso, cos
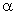 =
cos 90o = 0. Fica:
=
cos 90o = 0. Fica:
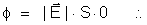
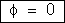
3o)
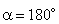 .
A superfície é novamente perpendicular ao campo, mas
o fluxo penetra pela face oposta àquela por onde penetrava
no 1o caso. Sendo
.
A superfície é novamente perpendicular ao campo, mas
o fluxo penetra pela face oposta àquela por onde penetrava
no 1o caso. Sendo
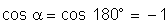 ,
fica:
,
fica:
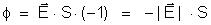
ou
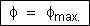
Vemos que, neste
caso, o fluxo é o máximo com sinal negativo.
4o)
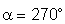 .
A superfície é novamente paralela ao campo. Neste
caso, cos
.
A superfície é novamente paralela ao campo. Neste
caso, cos
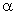 = cos 270o = 0. Fica:
= cos 270o = 0. Fica:

ou
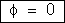
5o)
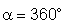 é a mesma posição de
é a mesma posição de
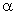 = 0o.
= 0o.
Representação
gráfica – Fazendo uma representação
gráfica do fluxo em função do ângulo
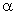 obtemos uma cosenoide, como indica a figura. Os máximos
dessa cosenoide correspondem ao valor
obtemos uma cosenoide, como indica a figura. Os máximos
dessa cosenoide correspondem ao valor
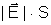 do fluxo; os mínimos, ao valor
do fluxo; os mínimos, ao valor
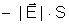 . . |
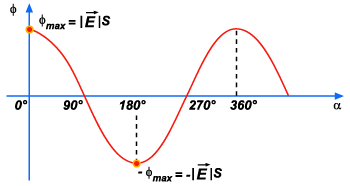 Figura 59 Figura 59 |