| |
[]
FenĂ´menos CrĂticos [P.M.C. de Oliveira]
FenĂ´menos CrĂticos
Invariância
por Transformaçþes de Escala
Paulo Murilo Castro de Oliveira
Instituto de FĂsica, Universidade Federal Fluminense, NiterĂłi, RJ
A figura 1 mostra o comportamento de um fluido
submetido a um processo de expansĂŁo isotĂŠrmica, temperatura constante.
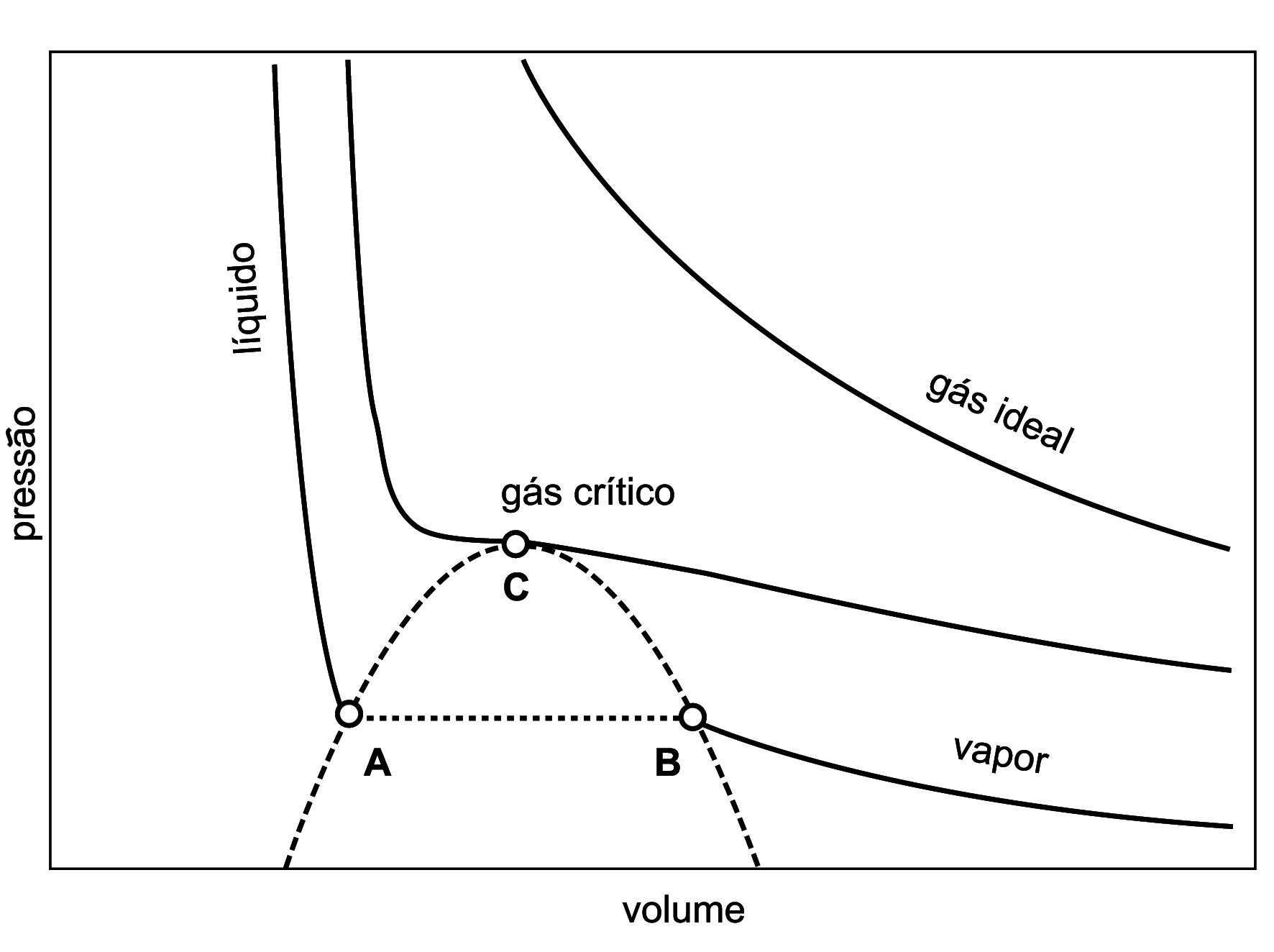
Figure 1. Queda de pressĂŁo de um fluido que se
expande em equilĂbrio tĂŠrmico. Para temperatura alta, o fluido ĂŠ um gĂĄs
ideal. Para temperatura baixa, o lĂquido evapora. HĂĄ uma temperatura
crĂtica intermediĂĄria, acima da qual o fluido ĂŠ um gĂĄs homogĂŞneo. A
separação de fases, lĂquido e vapor, sĂł ocorre abaixo desta temperatura
crĂtica. A curva de coexistĂŞncia, tracejada, ĂŠ o limite de estabilidade
destas fases, lĂquido Ă esquerda, vapor Ă direita. Abaixo, nĂŁo hĂĄ
equilĂbrio possĂvel de uma Ăşnica fase homogĂŞnea, a amostra se segrega em
duas porçþes, lĂquido (ponto
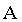 ) e vapor (ponto ) e vapor (ponto
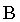 ). ).
No texto a seguir,
usarei este sistema e sua representação gråfica bastante conhecida como
protĂłtipos de uma classe muito mais ampla de sistemas onde os fenĂ´menos
crĂticos se manifestam.
A figura 1 representa
trĂŞs curvas relativas Ă citada expansĂŁo isotĂŠrmica do fluido, para trĂŞs
diferentes valores de temperatura. Quando a temperatura ĂŠ
suficientemente alta, curva superior, o fluido em questĂŁo estarĂĄ
necessariamente na fase gasosa, jamais se liquefaz. As inĂşmeras e
minĂşsculas molĂŠculas que o compĂľem se movimentam caoticamente, e colidem
com as paredes do recipiente. O efeito macroscĂłpico dessas colisĂľes ĂŠ a
pressão indicada no eixo vertical. A energia potencial de interação
entre essas molĂŠculas ĂŠ pequena, comparada com o valor tĂpico de sua
energia cinĂŠtica, este muito maior devido Ă alta temperatura. No caso
limite de temperaturas muito altas, costuma-se desprezar completamente a
energia de interação, levando em conta apenas a energia cinÊtica do
agitado movimento caĂłtico das molĂŠculas. Ă o chamado modelo de gĂĄs
ideal, estudado nas aulas de FĂsica do ensino mĂŠdio. Na figura 1, a
curva superior corresponde Ă famosa lei de Boyle, do sĂŠculo XVII, que
relaciona a pressĂŁo
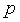 e o volume e o volume
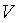 do gĂĄs ideal, na forma do gĂĄs ideal, na forma
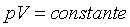 . Esta . Esta
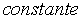 , por sua vez, ĂŠ proporcional Ă temperatura absoluta , por sua vez, ĂŠ proporcional Ă temperatura absoluta
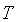 , mantida constante durante a expansĂŁo. Neste modelo
de gås ideal, a estrutura interna das molÊculas Ê irrelevante, uma vez que sua interação mútua foi completamente desprezada.
Qualquer que seja o gĂĄs em estudo, , mantida constante durante a expansĂŁo. Neste modelo
de gås ideal, a estrutura interna das molÊculas Ê irrelevante, uma vez que sua interação mútua foi completamente desprezada.
Qualquer que seja o gĂĄs em estudo,
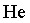 , ,
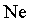
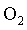
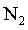
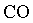
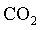
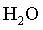
 , o comportamento ĂŠ o mesmo. NĂŁo ĂŠ preciso especificar
qual ĂŠ o gĂĄs ideal em estudo, qualquer gĂĄs cuja temperatura ĂŠ
suficientemente alta se comporta como o gĂĄs ideal do modelo. (Apenas
os efeitos de rotação e vibração das molÊculas, que têm influência na
proporcionalidade entre temperatura e energia, podem distinguir gases
monoatĂ´micos de diatĂ´micos, etc. PorĂŠm, este detalhe nĂŁo nos interessa
aqui.)
, o comportamento ĂŠ o mesmo. NĂŁo ĂŠ preciso especificar
qual ĂŠ o gĂĄs ideal em estudo, qualquer gĂĄs cuja temperatura ĂŠ
suficientemente alta se comporta como o gĂĄs ideal do modelo. (Apenas
os efeitos de rotação e vibração das molÊculas, que têm influência na
proporcionalidade entre temperatura e energia, podem distinguir gases
monoatĂ´micos de diatĂ´micos, etc. PorĂŠm, este detalhe nĂŁo nos interessa
aqui.)
Para baixas temperaturas,
curva inferior, a interação de cada molÊcula com as demais passa a ser
importante. Como esta interação geralmente Ê atrativa, caso a pressão no
interior do recipiente seja suficientemente alta, estas molĂŠculas tendem
a se movimentar menos livremente que no caso do gĂĄs, mais prĂłximas umas
das outras: ĂŠ o estado lĂquido, como ĂĄgua numa panela, por exemplo.
Comparada ao gĂĄs, a compressibilidade do lĂquido ĂŠ muito reduzida, como
mostra a curva inferior da figura 1, em sua parte Ă esquerda, quase
vertical. O estudo dos lĂquidos ĂŠ muito mais complicado, especĂfico para
cada substância, uma vez que a estrutura microscópica interna das
molÊculas determina sua forma particular de interação e,
conseqĂźentemente, o comportamento da energia potencial que descreve esta
interação. Pode-se fornecer calor ao lĂquido, mesmo mantendo sua
temperatura constante, como mostra a curva inferior da figura 1. Neste
caso, a energia tĂŠrmica ĂŠ usada para amenizar a tendĂŞncia das molĂŠculas
de se aglomerarem prĂłximas umas das outras, gerando uma pequena expansĂŁo
do lĂquido, que se observa na figura 1 ao descer a parte quase vertical
da curva inferior. Atingido o ponto
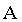 , a compactação das molÊculas Ê definitivamente
quebrada em algumas posiçþes do lĂquido, que ferve: bolhas de vapor
começam a aparecer no seu interior, com o volume especĂfico do ponto
, a compactação das molÊculas Ê definitivamente
quebrada em algumas posiçþes do lĂquido, que ferve: bolhas de vapor
começam a aparecer no seu interior, com o volume especĂfico do ponto
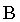 ,
muito mais rarefeitas que a parte ainda lĂquida.
AlĂŠm da temperatura constante, durante a fervura, lĂquido e vapor
coexistem dentro do mesmo recipiente, submetidos Ă mesma pressĂŁo
constante. Ă o caso da ĂĄgua fervente no nĂvel do mar, Ă pressĂŁo de ,
muito mais rarefeitas que a parte ainda lĂquida.
AlĂŠm da temperatura constante, durante a fervura, lĂquido e vapor
coexistem dentro do mesmo recipiente, submetidos Ă mesma pressĂŁo
constante. Ă o caso da ĂĄgua fervente no nĂvel do mar, Ă pressĂŁo de
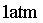 e com temperatura de e com temperatura de
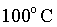 . A porção lĂquida (ponto
. A porção lĂquida (ponto 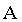 ) diminui gradativamente, dando origem a uma
quantidade crescente de vapor (ponto ) diminui gradativamente, dando origem a uma
quantidade crescente de vapor (ponto 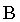 ). AlÊm de quebrar a ligação atrativa entre as
molĂŠculas, a energia tĂŠrmica absorvida durante este processo de fervura
Ê usada tambÊm para realizar o trabalho mecânico devido à expansão do
volume total. Exaurida a porção lĂquida, a amostra volta a ser homogĂŞnea,
apenas vapor, e se expande de forma semelhante a um gĂĄs, Ă direita do
ponto ). AlÊm de quebrar a ligação atrativa entre as
molĂŠculas, a energia tĂŠrmica absorvida durante este processo de fervura
Ê usada tambÊm para realizar o trabalho mecânico devido à expansão do
volume total. Exaurida a porção lĂquida, a amostra volta a ser homogĂŞnea,
apenas vapor, e se expande de forma semelhante a um gĂĄs, Ă direita do
ponto
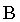 na figura 1.
na figura 1.
O fenĂ´meno crĂtico
ocorre na região intermediåria, na transição entre o regime de
temperaturas baixas descrito no parĂĄgrafo anterior e o regime de
temperaturas altas do penĂşltimo parĂĄgrafo. Na figura 1, essa regiĂŁo se
localiza nas proximidades do ponto
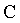 , denominado ponto crĂtico. Ele define precisamente a
temperatura crĂtica
, denominado ponto crĂtico. Ele define precisamente a
temperatura crĂtica
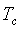 , que divide esses dois regimes, uma Ăşnica fase gasosa
e homogĂŞnea acima dessa temperatura, contra a possibilidade de
coexistĂŞncia de duas fases, lĂquido e vapor segregados no interior do
mesmo recipiente, abaixo.
, que divide esses dois regimes, uma Ăşnica fase gasosa
e homogĂŞnea acima dessa temperatura, contra a possibilidade de
coexistĂŞncia de duas fases, lĂquido e vapor segregados no interior do
mesmo recipiente, abaixo.
Do ponto de vista prĂĄtico, a importância dessa regiĂŁo crĂtica reside
na possibilidade de se efetuar enormes mudanças no sistema atravÊs de
pequenas variaçþes de um parâmetro de controle. No caso do gĂĄs crĂtico,
nas proximidades do ponto
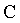 , um pequeno decrÊscimo da pressão (parâmetro de
controle) gera uma enorme expansĂŁo do volume do gĂĄs. Note que a isoterma
crĂtica, na figura 1, passa por um ponto de inflexĂŁo horizontal
justamente em
, um pequeno decrÊscimo da pressão (parâmetro de
controle) gera uma enorme expansĂŁo do volume do gĂĄs. Note que a isoterma
crĂtica, na figura 1, passa por um ponto de inflexĂŁo horizontal
justamente em
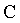 : neste ponto, portanto, a compressibilidade do fluido
Ê infinita, como resposta a uma pequena variação de pressão. Vårios
outros sistemas completamente diferentes tambĂŠm apresentam uma regiĂŁo
crĂtica com as mesmas caracterĂsticas. Por exemplo, toda a eletrĂ´nica
moderna se baseia em dispositivos, cuja curva caracterĂstica, voltagem
no eixo vertical contra corrente elĂŠtrica no eixo horizontal, apresenta
um ponto de inflexĂŁo horizontal. Desta forma, minĂşsculas correntes
elĂŠtricas (que codificam o bit dos computadores digitais) podem ser rapidamente
transformadas em correntes muito maiores (que codificam o bit
: neste ponto, portanto, a compressibilidade do fluido
Ê infinita, como resposta a uma pequena variação de pressão. Vårios
outros sistemas completamente diferentes tambĂŠm apresentam uma regiĂŁo
crĂtica com as mesmas caracterĂsticas. Por exemplo, toda a eletrĂ´nica
moderna se baseia em dispositivos, cuja curva caracterĂstica, voltagem
no eixo vertical contra corrente elĂŠtrica no eixo horizontal, apresenta
um ponto de inflexĂŁo horizontal. Desta forma, minĂşsculas correntes
elĂŠtricas (que codificam o bit dos computadores digitais) podem ser rapidamente
transformadas em correntes muito maiores (que codificam o bit 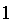 ), atravĂŠs de um pequenĂssimo aumento de voltagem, e
vice-versa. Outro exemplo sĂŁo os materiais gelatinosos que se usam para
construir micromotores e músculos artificiais: pequenas variaçþes na
acidez do ambiente (pH) geram enormes expansĂľes no volume desses
materiais, o que permite a realização de trabalho mecânico. ), atravĂŠs de um pequenĂssimo aumento de voltagem, e
vice-versa. Outro exemplo sĂŁo os materiais gelatinosos que se usam para
construir micromotores e músculos artificiais: pequenas variaçþes na
acidez do ambiente (pH) geram enormes expansĂľes no volume desses
materiais, o que permite a realização de trabalho mecânico.
Mais informaçőes
|
|