| |
[] Caos em Sistemas DinĂąmicos [A. P. S. de Moura; C. Grebogi]
Caos em Sistemas DinĂąmicos
Alessandro P.S. de Moura; Celso Grebogi
Instituto de FĂsica, Universidade de SĂŁo Paulo,
SĂŁo Paulo, SP
Desde o século XIX jå era
conhecido o fato de que a dinĂąmica de alguns sistemas fĂsicos determinĂsticos
pode ser bastante sensĂvel Ă s condiçÔes iniciais. No entanto, a importĂąncia e a
generalidade deste fato só começou a emergir a partir do trabalho de Poincaré em
mecùnica celeste [1]. Poincaré foi o primeiro a analisar sistemas dinùmicos
descritos por equaçÔes diferenciais ordinårias usando métodos globais e
qualitativos, atravĂ©s dos quais o comportamento de famĂlias de soluçÔes pode ser
estudado. Usando este tipo de mĂ©todo, Ă© possĂvel demonstrar que, em sistemas
dinùmicos autÎnomos (que não dependem do tempo) descritos por equaçÔes
diferenciais cujo espaço de fase tem duas dimensÔes, o comportamento assintótico
das trajetĂłrias Ă© simples, restringindo-se essencialmente a pontos fixos e
ciclos-limite (este resultado é demonstrado através do que hoje é conhecido como
o teorema de Poincaré-Bendixon). Poincaré descobriu, no entanto, que, em
sistemas de maior dimensionalidade, comportamentos extremamente complexos podem
acontecer. Analisando o problema dos trĂȘs corpos restrito, ele demonstrou que as
trajetĂłrias na vizinhança de certas Ăłrbitas, chamadas Ăłrbitas homoclĂnicas,
sĂŁo extremamente complexas. Este resultado pode ser considerado o marco inicial
da ĂĄrea de sistemas dinĂąmicos caĂłticos.
O progresso nesta ĂĄrea continuou
com o trabalho de Birkhoff [2], que ajudou a elucidar em detalhes a estrutura
das trajetĂłrias perto das Ăłrbitas homoclĂnicas. A generalidade e importĂąncia
destes resultados foram enfatizadas mais tarde pelo importante trabalho de Smale [3].
Ele demonstrou que, na região do espaço de fase próxima de uma órbita
homoclĂnica, a dinĂąmica Ă© topologicamente equivalente a um simples mapeamento do
plano, conhecido como a ferradura de Smale, que pode ser inteira e
rigorosamente analisado. Utilizando este mapeamento, Smale demonstrou, entre
outras coisas, que perto de qualquer Ăłrbita homoclĂnica existe um conjunto
infinito e enumerĂĄvel de Ăłrbitas periĂłdicas, com perĂodos arbitrariamente longos;
existe um conjunto infinito e nĂŁo-enumerĂĄvel de Ăłrbitas aperiĂłdicas; Ăłrbitas
inicialmente prĂłximas afastam-se uma da outra exponencialmente; e muitos outros
resultados.
Os trabalhos iniciais de
Poincaré e Birkhoff lidavam com sistemas Hamiltonianos, em que a dinùmica
preserva o volume do espaço de fase. No entanto, Cartwright e Littlewood [4],
juntamente com Levinson [5], mostraram que Ăłrbitas homoclĂnicas, assim como a
rica dinùmica associada a elas, estão presentes também em sistemas dinùmicos
dissipativos. Eles estudaram a equação de Van der Pohl, que descreve o
comportamento de um circuito elétrico não-linear com dinùmica dissipativa, e
mostraram a existĂȘncia de Ăłrbitas homoclĂnicas.
Somente a existĂȘncia de Ăłrbitas
homoclĂnicas nĂŁo implica necessariamente que a dinĂąmica assintĂłtica (para
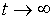 )
seja caĂłtica, pois as Ăłrbitas caĂłticas podem representar um
movimento transiente. No entanto, mesmo neste caso, a presença de caos tem
implicaçÔes profundas para a dinùmica. Se, por exemplo, um sistema dissipativo
tiver mĂșltiplos atratores, mesmo que cada um deles seja regular, a fronteira no
espaço de fase entre suas bacias de atração pode ter uma estrutura complexa
(ÂfractalÂ). Isto leva a uma grande indeterminação no estado final do sistema
(ou seja, para qual atrator uma dada condição inicial irå). Este comportamento é
chamado de caos transiente, e ele também acontece em sistemas
espalhadores, sendo neste contexto conhecido como espalhamento caĂłtico. )
seja caĂłtica, pois as Ăłrbitas caĂłticas podem representar um
movimento transiente. No entanto, mesmo neste caso, a presença de caos tem
implicaçÔes profundas para a dinùmica. Se, por exemplo, um sistema dissipativo
tiver mĂșltiplos atratores, mesmo que cada um deles seja regular, a fronteira no
espaço de fase entre suas bacias de atração pode ter uma estrutura complexa
(ÂfractalÂ). Isto leva a uma grande indeterminação no estado final do sistema
(ou seja, para qual atrator uma dada condição inicial irå). Este comportamento é
chamado de caos transiente, e ele também acontece em sistemas
espalhadores, sendo neste contexto conhecido como espalhamento caĂłtico.
Mais informaçőes
[1] H. PoincarĂ©, ÂLes mĂ©thodes nouvelles de
la mĂ©canique celesteÂ, Paris, Gauthier-Villars et fils (1899).
[2]
G.D. Birkhoff, ÂDynamical systemsÂ, American Mathematical Society, Colloquium
publications vol. , New York (1960).
[3]
S. Smale, Bull. Am. Math. Soc. , 747 (1967).
[4]
M.L. Cartwright, J. E. Littlewood, London Math. Soc. , 180 (1945).
[5]
N. Levinson, Ann. Math. , 127 (1949).
|
|